Обеспечивающие репрезентативность выборки
Чтобы выборка полно и адекватно представляла свойства генеральной совокупности, она должна быть представительной или репрезентативной. Репрезентативность может быть обеспечена только при объективности отбора данных.
Различают два вида выборочного наблюдения: повторный и бесповторный отбор.
При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора отобранная единица возвращается в совокупность и снова может быть выбранной - это «схема возвратного шара».
При бесповторном отборе отобранная единица не возвращается обратно, вероятность попадания остающихся единиц в выборку все время меняется - это «схема безвозвратного шара».
Способы отбора единиц из генеральной совокупности:
- индивидуальный отбор – в выборку отбираются отдельные единицы;
- групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц;
- комбинированный отбор – это комбинация первых двух.
Возможны следующие методы отбора единиц для формирования выборочной совокупности:
- случайный (непреднамеренный) отбор – при этом выборочная совокупность образуется с помощью жеребьевки или таблицы случайных чисел. Условием репрезентативности случайной выборки является то, что каждая единица имеет равную возможность попадания в выборку;
- механический – при этом выборочная совокупность определяется из генеральной, разбитой на равные интервалы (группы). Размер интервала равен обратной величине доли выборки: при 5% выборке отбирается каждая 20-я единица (1:0,05). Для обеспечения репрезентативности все единицы генеральной совокупности должны располагаться в определенном порядке. При этом отбор начинается не с первой единицы совокупности, а с середины первого интервала;
- типический (расслоенный, стратифицированный) – предполагает предварительное расчленение генеральной совокупности на качественно однородные типические группы (не обязательно равные). Затем отбор в выборочную совокупность из генеральной производится из типических групп при помощи случайного или механического отбора. Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Она дает более точные результаты по сравнению с другими способами отбора;
- серийная, или гнездовая, выборка – при этом из генеральной совокупности отбираются не отдельные единицы, а серии. Внутри каждой из попавшей в выборку серии обследуются все без исключения единицы.
Ошибка репрезентативности
При использовании выборочного метода возникает так называемая ошибка репрезентативности – это расхождение между характеристиками выборки и генеральной совокупности. Она зависит от численности выборки, вариации признака, методов отбора единиц выборочной совокупности и т.д. Ошибка может быть рассчитана по формуле:
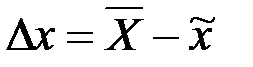 ,
,  , (6.1)
, (6.1)
При 
 , (6.2)
, (6.2)
 , (6.3)
, (6.3)
Ошибка репрезентативности является результатом того, что выборочная совокупность не полностью отражает закономерности, присущие всей генеральной совокупности. Методы математической статистики дают возможность измерить эту ошибку и указать границы ее колеблемости.
Можно построить ряд распределения выборок по величине ошибки репрезентативности для разных показателей. При бесконечно большом числе выборок получится кривая частот, называемая кривой выборочного распределения. Частота здесь – число выборок с той или иной ошибкой репрезентативности.
Если рассмотреть выборочное распределение средней величины, то оно будет приближаться к нормальному по мере увеличения объема выборки, независимо от распределения генеральной совокупности. С увеличением численности выборки величина выборочной средней будет приближаться к генеральной средней.
Рассчитывают два вида ошибок:
- среднюю (m),
- предельную (D).
Таблица 6.1
Расчет средней ошибки
| Способ отбора | Средняя (стандартная) ошибка (m) | |
| для средней | для доли | |
| Повторный | 
| 
|
| Бесповторный | 
| 
|






