Порядок расчета ошибок выборки для средней

 

1. По данным выборочного наблюдения устанавливается величина выборочной средней () и дисперсии.

2. Определяется средняя ошибка выборки

а) для повторного отбора:

 

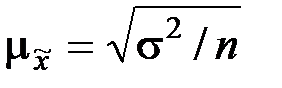, (6.4)

 

б) для бесповторного отбора (согласно исходным данным):

 

, (6.5)

 

где 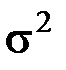- выборочная дисперсия.

3. С заданной вероятностью Р(t) находится предельная ошибка выборки:

 

, (6.6)

 

где t – коэффициент доверия,

- предельная ошибка выборки.

Множитель t определяется в зависимости от того, с какой доверительной вероятностью Р(t) надо гарантировать результаты выборочного наблюдения. На практике пользуются готовыми таблицами значений (табл. 6.2.).

Таблица 6.2

 

Коэффициент доверия t	Вероятность Р(t)
0,0 0,5 1,0 1,5 2,0 3,0	0,000 0,383 0,683 0,866 0,954 0,997

 

4. Доверительные пределы, в которых следует ожидать генеральную среднюю, составляют:

 

, (6.7)

 

Формула предельной ошибки выборочной средней (доли) позволяет решить следующие группы задач:

1) определять предел возможной ошибки средней или доли, т.е. величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;

2) рассчитывать оптимальную численность выборки, обеспечивающую требуемую точность;

3) определять вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.

 

Порядок расчета ошибок для доли

1. По данным выборочного наблюдения рассчитывается величина выборочной доли: ,

где m – численность единиц выборочной совокупности, обладающих данным признаком; n – численность выборочной совокупности.

2. Находится средняя ошибка для доли:

а) при повторном отборе:

 

, (6.8)

 

, (6.9)

 

3. С заданной вероятностью P(t) находится предельная ошибка выборки для доли:

 

, (6.10)

 

4. Предельные границы, в которых следует ожидать генеральную долю, составят:

 

, (6.11)

 

Расчет относительной ошибки выборки производится по формулам:

а) для средней:

 

, (6.12)

 

б) для доли:

 

, (6.13)

 

При отн. < 5%, выборка репрезентативна для оценки и расчета средних показателей по совокупности.

При 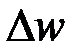отн. < 5%, выборка репрезентативна для оценки доли.

При отн. и отн. > 5% можно сделать вывод о нерепрезентативности выборки.

 

Конечная цель выборочного наблюдения заключается в распространении полученных данных на генеральную совокупность. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.

В зависимости от цели исследования применяются различные способы получения характеристик генеральной совокупности по показателям выборки.

При способе прямого пересчета показатель по генеральной совокупности рассчитывается путем умножения средних размеров признака (доли), найденных в результате выборочного обследования с учетом их предельной ошибки, на численность единиц генеральной совокупности. Расчеты ведутся по формулам:

 

, (6.14)

 

, (6.15)

 

Способ поправочных коэффициентов применяется в случаях, когда целью выборочного наблюдения является уточнение данных сплошного учета. Рассчитывается поправочный коэффициент путем сопоставления данных контрольного выборочного наблюдения и показателей сплошного наблюдения. Далее величина объема генеральной совокупности корректируется на поправочный коэффициент.