| Группы банков по размеру прибыли, млн. руб. | Число банков
| Середина интервала, млн. руб.
| 
| 
| 
| Накоп-ленные частоты
|
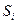
| Итого |
4. Вычислить эмпирическое корреляционное отношение 
:
,
где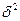 
– межгрупповая дисперсия прибыли;
– общая дисперсия прибыли (см. значение 
из п. 3).
Межгрупповая дисперсия прибыли вычисляется по формуле:
,
где 
– число банков в группах по размеру уставного капитала;
– групповые средние величины прибыли;
– общая средняя величина прибыли (см. значение 
из п. 1).
Расчет 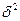оформить в табл. 2.3 (первые три графы табл. 2.3 заполняются на основе табл. 1.4):
Таблица 2.3
Расчет межгрупповой дисперсии прибыли
| Группы банков по размеру уставного капитала, млн. руб. | Число банков
| Средняя прибыль,
млн. руб.
|
|
|
|
| Итого | 
| - | - |
Произведя расчет эмпирического корреляционного отношения, оцените тесноту связи между размерами уставного капитала и прибыли банков по шкале Чеддока:
|
| 0.1 – 0.3 | 0.3 – 0.5 | 0.5 – 0.7 | 0.7 – 0.9 | 0.9 – 0.99 |
| Сила связи | Слабая | Умеренная | Заметная | Высокая | Весьма высокая |
Задание 3. Анализ факторных связей методами регрессии и корреляции
Проанализируйте взаимосвязь между размерами уставного капитала и прибыли по группе банков методами регрессии и корреляции. Сформулируйте выводы.
В качестве исходного материала используйте данные к заданию 1 (первые по порядку 10 банков).
Методические рекомендации
После ознакомления с темой «Статистический анализ взаимосвязей социально-экономических явлений» для выполнения задания студенту предлагается:
1. Представить график зависимости прибыли банков от размера уставного капитала на рис. 3 для уточнения формы связи между признаками. Точки, соответствующие значениям уставного капитала х и прибыли y, соединить отрезками прямой линии. Образованную на рисунке ломаную регрессии обозначить символом y. Используя графический метод, обосновать наличие прямолинейной зависимости между размером уставного капитала и прибылью банков.
2. Записать уравнение линейной регрессии, выражающее взаимосвязь между размерами уставного капитала и прибыли банков, в следующем виде:
Рассчитать параметры уравнения регрессии по методу наименьших квадратов, используя следующую систему нормальных уравнений:
,
где 
– теоретические значения прибыли;
– параметры уравнения регрессии;
– число единиц наблюдения (банков).
Решение указанной системы уравнений дает следующие формулы для нахождения параметров 
и 
:
;
.
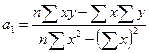Рассчитать коэффициент эластичности Э:
Интерпретировать значения параметра регрессии и коэффициента эластичности.
3. Вычислить теоретические значения прибыли по группе банков, последовательно подставляя исходные значения размеров уставного капитала х в уравнение регрессии с вычисленными параметрами. При правильно выполненных расчетах сумма теоретических значений прибыли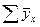 
совпадет с суммой ее фактических значений 
.
Теоретические значения прибыли представить графически в виде прямой линии, обозначенной на рис. 3 символом .
4. Рассчитать коэффициент корреляции r:
.
Сделать вывод о направлении и силе связи между размерами уставного капитала и прибыли банков.
5. Вычислить теоретическое корреляционное отношение R, предварительно рассчитав факторную 
и общую 
дисперсии прибыли:
;
;
.
Совпадение значений r и R должно подтвердить наличие линейной зависимости между признаками и правильность выполненных расчетов.
Результаты получить на основе расчетной табл. 3.1:
Таблица 3.1
