| Группы банков по размеру уставного капитала, млн. руб. | Число банков | Суммарная прибыль, млн. руб. | Средняя прибыль, млн. руб. (гр. 3: гр. 2) |
| 1 | 2 | 3 | 4 |
| Итого |
Для заполнения гр. 3 удобно воспользоваться записью данных в табл. 1.1. В итоговой строке гр. 4 приводится общая средняя величина прибыли на один банк.
Определить разновидность группировки, представленной в табл. 1.4. Сделать выводы о наличии и направлении связи между размером уставного капитала и величиной прибыли банков.
Задание 2. Расчет средних величин показателей вариации и
Эмпирического корреляционного отношения
Вычислите среднюю величину, моду, медиану, дисперсию, среднее квадратическое отклонение и коэффициент вариации прибыли банков по сгруппированным данным. Рассчитайте эмпирическое корреляционное отношение и оцените тесноту связи между размером уставного капитала и величиной прибыли банков. Сформулируйте выводы.
В качестве исходного материала используйте данные табл. 1.3.
Методические рекомендации
После ознакомления с темой «Метод средних величин и вариационный анализ» для выполнения задания студенту предлагается:
1. Рассчитать среднюю арифметическую величину прибыли способом моментов:
,
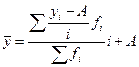где 
– средняя арифметическая;
– середины (средние значения) интервалов;
А – середина интервала, соответствующего наибольшей частоте;
– частоты (число банков в каждой группе);
i – величина интервала.
Объясните на данном примере целесообразность применения способа моментов в расчете средней величины.
2. Вычислить моду и медиану по следующей методике:
,
где 
– мода;
– нижняя граница модального интервала;
– величина модального интервала;
– частота модального интервала;
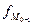– частота интервала, расположенного перед модальным;
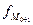– частота интервала, следующего за модальным.
,
где 
– медиана;
– нижняя граница медианного интервала;
– величина медианного интервала;
– накопленная частота интервала, расположенного перед медианным;
– частота медианного интервала.
Сравнить расчетное значение медианы с серединой ранжированного ряда банков по величине прибыли (в данном примере медиана равна средней арифметической прибыли двух банков, находящихся в середине ряда).
Охарактеризовать результаты вычислений.
3. Выполнить расчеты дисперсии, среднего квадратического отклонения и коэффициента вариации прибыли по методике, приведенной в табл. 2.1:
Таблица 2.1
Показатели вариации
| Показатели | Метод расчета |
1. Дисперсия 
| 
|
2. Среднее квадратическое
отклонение 
| 
|
3. Коэффициент вариации  
| 
|
Оценить однородность совокупности банков по размеру прибыли. Совокупность считается однородной, если 
не превышает 33%.
Для получения результатов рекомендуется использовать расчетную таблицу 2.2:
Таблица 2.2
