Каппа. Альфа уже сказал, что наш «старый» метод приводит к порочной бесконечности[173]. Гамма и Ламбда ответили надеждой, что поток опровержений может иссякнуть[174]; но теперь, когда мы понимаем механизм успеха опровержений – расширение понятий, – мы знаем, что их надежда была тщетной. Для всякого предложения всегда найдется некоторое достаточно узкое толкование его терминов, которое окажется истинным, и некоторое достаточно широкое, которое окажется ложным. Какое толкование предполагается, и какое нет, зависит, конечно, от наших намерений. Первое толкование можно было бы назвать догматическим, подтвердительным или оправдательным толкованием, а второе скептическим, критическим или опровергательным. Альфа назвал первое конвенционалистской стратагемой[175], но теперь мы видим, что второе будет таким же. Вы все осмеяли догматическое толкование Дельтой наивной догадки[176], а затем догматическое толкование Альфой теоремы[177]. Но расширение понятий опровергает всякое утверждение и вообще не оставит истинного утверждения.
Гамма. Постойте. Правда, мы расширили понятие «многогранник», затем разорвали его и отбросили; как указал Пи, наивное понятие «многогранник» уже не фигурирует больше в теореме.
Каппа. Но тогда вы начнете расширять термин в теореме – теоретический термин, не правда ли? Вы сами решили расширить «односвязную грань» так, чтобы включить круг в боковую поверхность цилиндра[178]. Вы подразумевали, что интеллектуальная честность требует подставить шею, добиться почетного статуса опровергаемости, т.е. сделать возможным толкование опровергателя. Но пои наличии расширения понятий опровергаемость означает опровержение. Таким образом, вы скользите по бесконечному склону, опровергая каждую теорему и заменяя ее более «строгой» – такой, ложность которой еще не выявлена. Но вы никогда не выйдете из ложности.
Сигма. А что, если мы остановимся на некотором пункте примем оправдательные толкования и не будем трогаться дальше от истины или от той частной лингвистической формы, в которой была выражена истина?
Каппа. Тогда вам придется отражать контрапримеры, расширяющие понятия, вместе с устраняющими монстры определениями. Таким образом, вы будете скользить по другому бесконечному склону: вы будете принуждены принимать каждую «особую лингвистическую форму» вашей истинной теоремы, которая не будет достаточно точной, и вы будете принуждены включать в нее все более и более.«строгие» определения, выраженные в терминах, неясность которых еще не разоблачена. Но вы никогда не выйдете из неясности.
Тета (в сторону). Что же плохо в эвристике, где неясность является ценой, которую мы платим за рост?
Альфа. Я сказал вам: точные понятия и непоколебимые истины живут только в мысли, но не в языке!
Гамма. Позвольте мне сделать вам вызов, Каппа. Возьмите теорему, как она стояла, после того как мы учли цилиндр: «Для всех простых объектов с односвязными гранями, у которых ребра оканчиваются в вершинах,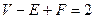 
. Как вы опровергнете это методом расширения понятий?
Каппа. Прежде всего я вернусь к определяющим терминам и произнесу предложение полностью. Затем я решу, какие понятия надо расширить. Например, «простой» стоит вместо «могущий быть растянутым в плоскости после отнятия одной грани». Я растяну термин «растягивание». Возьмите уже продискуссированные тетраэдры-близнецы, имеющие общее ребро (рис. 6, а). Этот многогранник будет простым, его грани – односвязными, но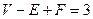 
Итак, наша теорема неверна.
Гамма. Но эти близнецы-тетраэдры не будут простым многогранником!
Каппа. Конечно, будут простым. Отнимая любую грань, я могу растянуть его на плоскости. Мне придется только быть осторожным, когда я подойду к критическому ребру, чтобы ничего не разорвать, открывая по этому ребру второй тетраэдр.
Рис. 24
Гамма. Но это же не растягивание! Вы режете – или расщепляете – ребро на два ребра. Вы, конечно, не можете поместить одну точку в двух точках: растягивание является дважды непрерывным однозначным отображением.
Каппа. Определение 9? Боюсь, что это узкое, догматическое толкование «растягивания» не удовлетворит моему здравому смыслу. Например, я вполне могу в воображении растянуть квадрат (рис. 24, а) в два вложенных друг в друга квадрата, если растяну его контурную линию (рис. 24, б). Назовите ли вы это растягивание разрезом или расщеплением только потому что оно не представляет «дважды непрерывного однозначного отображения». Между прочим, я удивляюсь, почему вы не определили растягивание как преобразование, которое оставляет V, E и F неизменными, и покончили бы с этим?
Гамма. Верно, вы опять выиграли. Я должен или согласиться с вашим опровергательным толкованием «растягивания» и расширить мое доказательство, или найти более глубокое, или включить лемму, или внести определение устраняющее монстры. Однако в каждом из этих случаев я всегда буду делать более и более ясным мои определяющие термины. Почему я не должен прийти к такой точке, для которой значение терминов будет настолько кристально ясным, что может быть только одно-единственное толкование, как в случае с 2+2=4? Здесь нет ничего эластичного в смысле этих терминов и ничего опровержимого в истине этого определения, которое вечно сияет в естественном свете разума.
Каппа. Мутный свет!
Гамма. Расширьте, если вы можете.
Каппа. Но это же детская игра! В некоторых случаях два и два составляют пять. Предположим, что просим прислать две вещи, из которых каждая весит два фунта; они были присланы в ящике, весящем один фунт; тогда в этой упаковке два фунта и два фунта составляют пять фунтов!
Гамма. Но вы получаете пять фунтов, складывая три груза, 2 и 2 и 1!
Каппа. Верно, наша операция «2 и 2 составляют 5» не представляет сложения в первоначальном смысле этого слова. Но простым расширением смысла сложения мы можем сделать этот результат истинным. Наивное сложение представляет очень частный случай упаковки, когда вес покрывающего материала равен нулю. Нам нужно включить эту лемму в догадку в качестве условия: наша исправленная догадка будет: «2+2=4 для «невесомого» сложения»[179]. Вся история алгебры представляет ряд таких расширений понятий и доказательств.
Гамма. Я думаю, что вы «растягиваете» слишком далеко. В следующий раз вы (истолкуете «плюс» как «косой крест» и будете рассматривать это как опровержение! Или вы истолкуете «все» как «не» в положении: все многогранники суть многогранники»! Вы расширяете понятие расширения понятий! Мы должны отграничить опровержение при помощи рационального расширения от «опровержения» при помощи иррационального расширения. Мы не можем позволить вам расширить любой термин так, как вы этого хотите.
Мы должны закрепить понятие контрапримера в кристально ясных терминах!
Дельта. Даже Гамма обратился в устранителя монстров: теперь для опровержения расширением понятий он хочет получить определение, устраняющее монстры. Разумность в конце концов зависит от неэластических, точных понятии[180].
Каппа. Но таких понятий не существует! Почему не принять, что наша способность уточнять смысл наших выражений ничтожна и поэтому наша способность доказывать тоже ничтожна? Если вы хотите, чтобы математика имела смысл, то вы должны отказаться от достоверности. Если вы хотите достоверности, избавьтесь от смысла. Вы не можете иметь и то и другое. Тарабарщина безопасна от опровержений, имеющие смысл предложения могут быть опровергнуты расширением понятий.
Гамма. Тогда ваши последние утверждения тоже могут быть опровергнуты – и вы знаете это. «Скептики – это не секта людей, убежденных в том, что они говорят, это – секта лжецов»[181].
Каппа. Ругательства – последнее прибежище разума!
