Линейная корреляционная зависимость, уравнение линейной регрессии

При рассмотрении двумерных случайных величин было введено понятие условного математического ожидания. Соответственно условное среднее по данным выборки называется выборочным уравнением регрессии случайной величины Y на случайную величину X.

Функция называется выборочной функцией регрессии, а ее график – выборочной линией регрессии. …

Аналогично функцию 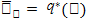называют выборочной функцией регрессии x на y.

Функция корреляции рассматривает задачи нахождения параметров распределения функций f и ϥ уточнения частоты связи между СВ и выяснение вопроса о виде корреляционной зависимости. Простейшей функцией регрессии является линейная функция, говорят, что две СВ связаны линейной регрессией, если уравнения y на x и x на y являются линейными. Для получения уравнения линейной регрессии используется метод наименьших квадратов.

Обозначим наблюдаемые значения Y₁, Y₂, …, Y_n.

Коэффициенты уравнения линейной регрессии находят из требования минимизации суммы квадратичного отклонения.

Из этой системы мы находим k и b и получаем уравнение линейной регрессии. Мы предполагаем, что каждому значению x соответствует единственное значение y.

…

Поэтому … данные задач линейной регрессии записываются в виде корреляционной таблицы, в которой указываются наблюдаемые значения x и y, и которые пары этих значений встретились в наблюдении.

y\x
		-
	-

 

По данным корреляционной таблицы уравнение корреляционной регрессии находится из системы нормальных уравнений, которые имеют вид.

 

1. Биномиальное и геометрическое распределения.(25)

2. Виды уравнений математической функции(12)

3. Дискретные случайные величины и способы их задания. Ряд распределения.(24)

4. Дисперсия случайной величины и её свойства. Среднеквадратическое отклонение.(33)

5. Доверительный интервал для неизвестного математического ожидания нормальной распределённой случайной величины при известной дисперсии(47)

6. Доверительный интервал для неизвестного математического ожидания нормальной распределённой случайной величины при не известной дисперсии(48)

7. Закон больших чисел. Теоремы Чебышева, Бернулли, Хинчина(40)

8. Интервальные оценки. Точка доверительной вероятности(46)

9. Классической определение вероятности(18)

10. Коэффициент ковариации случайных величин и её свойства(39)

11. Линейная корреляционная зависимость. Уравнение линейной регрессии(50)

12. Математическое ожидание случайной величины и её свойства(32)

13. Метод Даламбера. Решение уравнения колебаний для бесконечной струны(14)

14. Метод Фурье. Решение уравнения колебаний для конечной струны(15)

15. Метод Фурье. Решение уравнения теплопроводности для конечного стержня(16)

16. Непрерывные случайные величины способы их задания(27)

17. Нормальный закон распределения. Правило трёх сигм(30)

18. Общее понятие теории рядов. Сумма рядов. Свойства рядов. Необходимый признак сходимости числового функционального ряда.(1)

19. Операции над событиями(19)

20. Определение случайной величины. Функция распределения случайной величины и её свойства.(23)

21. Основные задачи математической статистики. Выборка в ковариационный ряд(41)

22. Плотность распределения случайной величины и её свойства(28)

23. Понятие о двумерной случайной величине. Функция распределения двумерной случайной величины и её свойства(34)

24. Понятие о преобразовании Фурье(11)

25. Предмет теории вероятности. Относительная частота. Понятие статистической устойчивости(17)

26. Представление функции в виде интеграла Фурье(10)

27. Равномерное и показательное распределения(29)

28. Разложение нечётной периодической функции на интервале [0;п](6)

29. Разложение периодической функции на интервале [–l;l](4)

30. Разложение периодической функции на интервале [–п;п](3)

31. Разложение функции в ряд по cos на интервале [0;п](9)

32. Разложение функции в ряд по sin на интервале [0;п](8)

33. Разложение функции в ряд по функциям ортогональной системы(7)

34. Разложение чётной периодической функции на интервале [0;п](5)

35. Распределение непрерывной двумерной случайной величины. Совместная плотность распределения и распределение компонент в отдельности.(36)

36. Распределение непрерывной случайной величины. Распределение компонент двумерной случайной величины.(35)

37. Распределение Пуассона(26)

38. Ряд Фурье для периодической функции.(2)

39. Стохастические и корреляционные зависимости(49)

40. Теоремы сложения и умножения вероятностей. Совместные и несовместные события. Зависимые и независимые события.(20)

41. Точечная оценка математического ожидания и её свойства(44)

42. Точечная оценка дисперсии. Формула для вычислений(45)

43. Точечная оценка параметров распределения(43)

44. Уравнение колебаний. Начальные и граничные условия. Задача Коши.(13)

45. Условие независимости и коррелированности случайных величин. Связь между этими понятиями.(37)

46. Формула Бернулли. Предельные теоремы Пуассона. Локальные и интегральные теоремы Муавра-Лапласса.(22)

47. Формула полной вероятности(21)

48. Числовые характеристики двумерной случайной величины. Математическое ожидание компонент, дисперсия и ковариационный момент(38)

49. Числовые характеристики случайных величин. Понятие о начальных и центральных моментах(31)

50. Эмпирическая функция распределения(42)