Доверительный интервал для неизвестного математического ожидания нормально распределенной случайной величины при известной дисперсии

Имеется генеральная совокупность, которая распределена по нормальному закону с известной дисперсией. Требуется по результатам выборки построить доверительный интервал для оценки неизвестного математического ожидания.

Dѯ = σ² Mѯ = a

x₁, x₂, …, x_n
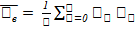– строим на основании выборки точечную оценку.

Пусть задана доверительная вероятность γ, т.е вероятность, с которой нам требуется гарантировать, что математическое ожидание а попадет в доверительный интервал.

,

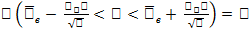Где Φ(t_γ) = γ, где Φ –функция Лапласа.

Для решения такого уравнения по таблице значений функции Лапласа нужно найти аргументы, при которых функция Лапласа принимает значение γ.

Число называется точностью оценки, легко видеть, что точность оценки возрастает, если уменьшается дисперсия, либо возрастает объем выборки.

Если точность оценки задана, то мы можем найти объем выборки, который гарантирует эту точность.

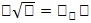
Доверительный интервал для неизвестного математического ожидания нормально распределенной случайной величины при неизвестной дисперсии

В большинстве практических задач известно, либо можно доказать, что СВ распределена по нормальному закону, но ни математическое, ин дисперсия для нее неизвестны, тогда использовать предложенный доверительный интервал нельзя. Потому, что для дисперсии также нужно найти точечную оценку. В этом случае доверительный интервал имеет вид:

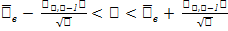, где S – точечная оценка исправленной выборочной дисперсии, a 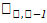находится по таблице распределения Стьюдента при заданном γ и заданном n, которое называется числом степеней свободы.

Стохастическая и корреляционная зависимость

При изучении различных зависимостей различают функциональную и стохастическую зависимость. В функциональной зависимости каждому значению переменной соответствует единственное значение функции, так как в математической статистике в основном рассматривают случайные величины, то функциональная зависимость используется очень редко, поэтому в основном изучают стохастическую зависимость.

Зависимость называется стохастической, если изменение одной из величин влечет изменение другой величины. Если при изменении одной из величин изменяется распределение другой, то такая зависимость называется корреляционной. Классическим примером корреляционной зависимости является зависимость урожайности от количества удобрений. Для выяснения корреляционной зависимости находят условные средние значения, которые вычисляются по данным выборки. 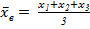– условное среднее.