Поглиблений аналіз структури передбачає оцінювання співвідношень, пропорцій між окремими складовими одного цілого. Такий різновид порівнянь називають відносною величиною координації. Вона показує, скільки одиниць однієї частини сукупності припадає на 1, 100 і 1000 одиниць іншої, узятої за базу порівняння. За даними попереднього прикладу на одиницю власних коштів припадає 0,47 залучених:
32: 68 = 0,47.
Комплексне використання відносних величин динаміки, структури та координації розглянемо на прикладі матеріальних запасів умовної фірми за 2 квартали (табл. 4.1).
Таблиця 4.1
МАТЕРІАЛЬНІ ЗАПАСИ ФІРМИ
| Матеріальні запаси | Запаси, тис. грн., на кінець кварталу | ІV квартал, % до ІІІ квар- талу | Структура запасів, % до підсумку кварталу | Структурні зрушення, п.п. | ||
| ІІІ | ІV | ІІІ | ІV | |||
| Сировина та напівфабрикати | 102,5 | –6 | ||||
| Готова продукція | 132,1 | +6 | ||||
| Разом | 112,0 |
За ІV квартал матеріальні запаси в цілому зросли в 1,12 раза або на 12%. Оскільки запаси складаються з двох функціонально відмінних складових, то потрібно оцінити динаміку кожної з них. Так, запаси сировини і напівфабрикатів зросли лише на 2,5%, а запаси готової продукції — на 32,1%. Нерівномірність динаміки окремих складових зумовила зміни в структурі матеріальних запасів. Якщо в ІІІ кварталі частка сировини та напівфабрикатів становила 68%, то в ІV кварталі зменшилась до 62%, тобто на 6 п. п. Відповідно на стільки ж зросла частка готової продукції. Внаслідок структурних зрушень змінились пропорції між складовими частинами: у ІІІ кварталі на 1 грн. запасів готової продукції припадало 2,125 грн. запасів сировини і напівфабрикатів (119: 56 = = 2,125), у ІV кварталі їх співвідношення зменшилося до 1,65 (122: 74 = 1,65).
Відносні величини інтенсивності
Особливим видом відносних показників є результат порівняння різнойменних абсолютних величин: у чисельнику — обсяги певного явища (кількість подій, фактів), у знаменнику — обсяг середовища, якому це явище (подія) властиве. У кожному конкретному випадку таке співвідношення характеризує інтенсивність поширення явища в середовищі, а тому називається відносною величиною інтенсивності. На відміну від відносних величин групи А відносні величини інтенсивності іменовані одиницями вимірювання чисельника і знаменника співвідношення. Наприклад, густота населення в регіоні — 82,5 осіб на 1 км2, виробництво електроенергії — 5627 кВт · год на душу населення і т. ін.
У формі відносних величин інтенсивності обчислюється низка показників технічного рівня виробництва (електроозброєність праці), ефективності використання ресурсів (фондовіддача), економічного розвитку країни (валовий внутрішній продукт на душу населення), життєвого рівня населення (забезпеченість сімей товарами культурно-побутового призначення), інших аспектів суспільного життя.
Якщо обсяги явища незначні відносно обсягів середовища, то результат їх співвідношення збільшується в 100, 1000 і більше разів. Так, демографічні явища (народжуваність, смертність, шлюбність) розраховуються на 1000 осіб, забезпеченість лікарями, підприємствами громадського харчування — на 10 000 осіб, захворюваність, злочинність — на 100 000 осіб. Такі показники називаються відповідно промілле, продецимілле, просантимілле.
У порівняльному аналізі використовуються кратні співвідношення не лише абсолютних величин. Комплексна й всебічна характеристика закономірностей суспільного життя передбачає порівняння середніх і відносних величин.
Середні величини
Середня величина є узагальнюючою мірою ознаки, що варіює, у статистичній сукупності. Показник у формі середньої характеризує рівень ознаки в розрахунку на одиницю сукупності. Як уже зазначалося, значення ознаки j -го елемента поєднує в собі як спільні для всієї сукупності типові риси, так і притаманні лише цьому елементу індивідуальні особливості. Абстрагуючись від індивідуальних особливостей окремих елементів, можна виявити те загальне, типове, що властиве всій сукупності.
Саме в середній взаємно компенсуються індивідуальні відмінності елементів та узагальнюються типові риси. Типовість середньої пов’язана з однорідністю сукупності. Середня характеризуватиме типовий рівень лише за умови, що сукупність якісно однорідна. У неоднорідній сукупності, за влучним висловом П. Самуельсона, осереднюються «тигри та кицьки», що лише створює ілюзію «благоденствія» і не віддзеркалює реалій.
Взаємозв’язок індивідуальних значень ознаки та середньої — це діалектична єдність загального і окремого. Замінюючи множину індивідуальних значень, середня не змінює визначальної властивості сукупності — загального обсягу явища. Зв’язок визначальної властивості з елементами сукупності описується функцією f (x 1, x 2,... xn), яка виражає певну математичну дію над емпіричними значеннями ознаки (підсумовування, множення, степенювання, коренювання) і визначає вид середньої. Так, у разі підсумовування значень ознаки визначальну властивість забезпечує середня арифметична, при множенні — середня геометрична і т. д.
Отже, при обчиᑁленні середніх у соціально-економічних дослідженнях необхідно чітко усвідомити визначальну властивість сукупності та логіко-математичну суть — логічну формулу — показника. Наприклад, логічна формула середнього вкладу в банк:
.
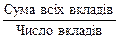Чисельник логічної формули середньої являє собою обсяг значень (визначальну властивість) ознаки, що варіює, а знаменник — обсяг сукупності. Як правило, визначальна властивість — це реальна абсолютна чи відносна величина, яка має самостійне значення в аналізі. У кожному конкретному випадку для реалізації логічної формули використовується певний вид середньої, зокрема:
а) середня арифметична;
б) середня гармонічна;
в) середня геометрична;
г) середня квадратична і т. д.
Залежно від характеру первинної інформації середня будь-якого виду може бути простою чи зваженою. Позначається середня символом 
(риска над символом означає осереднення індивідуальних значень) і вимірюється в тих самих одиницях, що й ознака.
Середня арифметична
Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, незгрупованими даними обчислюється середня арифметична проста:
Наприклад, за місяць страхова компанія виплатила страхове відшкодування за п’ять ушкоджених об’єктів на суму, тис. грн.: 18, 27, 22, 30, 23. Середня сума виплати страхового відшкодування, тис. грн.:
За формулою простої арифметичної обчислюються середні у динамічному ряду. Якщо в січні агрофірма продала молокозаводу 315, у лютому — 305, а в березні — 340 т молока, то середньомісячний продаж молока, т: (315 + 305 + 340): 3 = 320.
Моментні показники замінюються середніми як півсума значень на початок і кінець періоду. Якщо моментів більш ніж два, а інтервали часу між ними рівні, то в чисельнику до півсуми крайніх значень додають усі проміжні, а знаменником є число інтервалів, яке на одиницю менше від числа значень ознаки. Таку формулу називають середньою хронологічною:
Наприклад, на фірмі залишки обігових коштів на початок кожного місяця І кварталу становили, млн грн.: січень — 70, лютий — 82, березень — 77, квітень — 80. Середньомісячний залишок обігових коштів, млн грн.:
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2,..., m), а обсяг значень ознаки визначити як суму добутків варіант хj на відповідні їм частоти fj, тобто як 
. Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
Вагами можуть бути частоти або частки (відносні величини структури), іноді інші величини (абсолютні показники). Припустимо, у фірмі працює 20 налагоджувачів аудіо- та відеоапаратури, з них три мають 4-й розряд, дев’ять — 5-й, вісім — 6-й. Середній тарифний розряд
Середня не збігається з жодним значенням ознаки, але це типовий рівень кваліфікації налагоджувачів фірми.
Формально між середньою арифметичною простою і середньою арифметичною зваженою немає принципових відмінностей. Адже багаторазове (f раз) підсумовування значень однієї варіанти замінюється множенням варіант х на вагу f. Проте функціонально середня зважена більш навантажена, оскільки враховує поширеність, повторюваність кожної варіанти і певною мірою відображує склад сукупності. Значення середньої зваженої залежить не лише від значень варіант, а й від структури сукупності. Чим більшу вагу мають малі значення ознаки, тим менша середня, і навпаки. Наприклад, незважаючи на той факт, що в двох регіонах мешкають люди різного віку, у тому регіоні, де більше дітей, середній вік населення буде менший. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі сукупностей, склад яких істотно різний. У таких випадках, аби елімінувати (усунути) вплив структури сукупності на середню, вдаються до пошуку стандартизованих ваг.
У структурованій сукупності при розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні 
, кожна з яких має відповідну вагу у вигляді групових частот fj:
Обчислену так середню на відміну від групових називають загальною.
Як приклад використаємо групові середні альтернативної ознаки, яка набуває взаємовиключних значень 1 або 0. Відповідні цим значенням частоти f 1 та f 0. Очевидно, середня такої ознаки є часткою d 1:
Так, за даними перепису населення в регіоні проживало 5,2 млн осіб, із них у містах — 3,5, у сільській місцевості — 1,7. Частка осіб працездатного віку відповідно становила 0,60 та 0,48.
Середня частка населення працездатного віку в регіоні є арифметичною зваженою з групових часток:
Середня арифметична має певні властивості, які розкривають її суть.
1. Алгебраїчна сума відхилень окремих варіант ознаки від середньої дорівнює нулю:
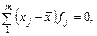
тобто в середній взаємно компенсуються додатні та від’ємні відхилення окремих варіант.
2. Сума квадратів відхилень окремих варіант ознаки від середньої менша, ніж від будь-якої іншої величини:
3. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А або в А раз, то й середня зміниться аналогічно.
Ця властивість найвиразніше ілюструється на прикладі ознак порядкової (рангової) шкали, для якої використовуються різні варіанти оцифрування. Так, окремим пунктам 3-бальної шкали можна надати значень 1, 2, 3 або –1, 0, 1. Очевидно, розраховані для цих варіант оцифрування середньозважений 
та середній центрований 
бали відрізнятимуться на величину А = 2. Так, за даними табл. 4.2 оцінимо ставлення населення до смертної кари.
Таблиця 4.2
