ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Санкт-Петербург
Введение
Эффективная организация обмена информацией – необходимое условие успешной практической деятельности людей. Основой для передачи является электросвязь. Системы электросвязи стандартизованы по видам связи на телефонные, телеграфные, фототелеграфные, звукового вещания, телевидения и передачи данных. Последняя из систем – объект изучения данного курса.
Каналы передачи данных и их математические модели.
Основные определения.
Под информацией будем понимать сведения о ком-либо, о чем-либо. Это результат отражения материального мира.
Форма представления информации (текст, изображение, речь) – сообщение. Множество возможных сообщений с их вероятностными характеристиками – называют ансамблем сообщений. Выбор сообщений из ансамбля осуществляет источник сообщений. Процесс выбора является случайным. Сообщения передаются от источника к получателю (адресату) при помощи сигналов.
Сигнал – это физический процесс, который однозначно с заданной точностью отображает сообщение и служит для переноса информации в пространстве и времени. Формирование сигнала сводится к двум операциям кодированию и модуляции. Кодирование в широком смысле – это преобразование сообщения в сигнал. По существу кодирование сводится к составлению и хранению некоторой таблицы типа «что» А есть «что» Z. Так как А велико, то сообщения расчленяют на элементарные сообщения буквы и кодируют первоначально именно буквы. Это кодирование в узком смысле.
Код – универсальный способ отображения информации при ее хранении, обработке, передачи в виде системы соответствий между элементами сообщений и сигналами, при помощи которых эти элементы можно зафиксировать.
Основными параметрами кода являются его основание и значность. Основание кода (q) равно числу различных символов первичного алфавита. Можно указать два крайних случая представления М различных символов первичного алфавита в виде сигналов -двоичное и М-ичное. В первом случае, все элементы первичного алфавита нумеруются в двоичной системе счисления и таким образом представляются в виде последовательности нулей и единиц (код комбинированный). Значность кода (n) при этом находится из соотношения: 2 n ³ М. При М-ичном кодировании каждой букве первичного алфавита xi сопоставляется свой сигнал Si (t) длительностью Tc. Для двоичного кода q=2, для М-ичного q=М.
Чтобы кодовые комбинации преобразовать в сигнал, пригодный для передачи используют операцию модуляции (манипуляции).
Модуляция – это изменение одного или нескольких параметров сигнала-переносчика в соответствии с передаваемыми сообщениями. Основное назначение модуляции – согласование на физическом уровне источника информации с каналом (линией) связи.
Совокупность операций, связанных с преобразованием передаваемых сообщений в сигнал, называется способом передачи. Описать его математически можно операторным соотношением:
{Ski(t)} = Dпер{xi} = DмDк {xi}
Линия связи – среда распространения сигналов, включающая усилительные и регенерационные пункты.
Сформированные сигналы излучаются в среду распространения (линию связи), где они ослабляются и искажаются. Поэтому в точке приема будут наблюдаться сигналы 
отличные от переданных не только энергией.
Влияние линии связи на сигнал можно задать операторным соотношением:
= Dс{ Ski(t)} = DсDпер {xi}.
Кроме искажений сигнала на входе приемного устройства имеются еще помехи и аддитивные шумы самого приемника, так что наблюдается непрерывный сигнал 
.
Смесь сигнала и помех должна быть преобразована в дискретные сообщения, соответствующие переданным. Эти операции сводятся к демодуляции и декодированию - обратным модуляции и кодированию.
Совокупность технических средств и среды распространения, обеспечивающих передачу сигналов между источником и адресатом называют каналом связи.
Системой связи - совокупность канала связи, источника и получателя, характеризующаяся определенными способами преобразования сообщения в сигнал и восстановления сообщения по принятому сигналу.
Процесс передачи сообщений в общем виде можно представить приведенной ниже совокупностью преобразований: 
После фильтрации и усиления в приемном устройстве сигнал демодулируется. Образуется дискретная последовательность 
, которая должна соответствовать последовательности {xki}. Однако из-за помех, влияния среды, погрешностей преобразования полного соответствия и {xki} может не быть. Далее декодер преобразует в {xki} соответствующие {xi}. Способ приема – это совокупность операций по преобразованию сигналов и помех в дискретные сообщения:
{xi}= Dпр [y(t)] = Dпр[ + 
] = Dдк Dдм[ + ]
Весь процесс передачи в операторной форме можно представить как
{ 
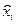}= Dпр [Dс Dпер{xi} + ] = Dдк Dдм[Dс Dм Dк{xi}+ ].
Нас будет интересовать одна из систем электросвязи - система передачи данных (СПД). Термин данные определен как машинные (цифровые) сообщения.
Общая задача СПД заключается в доставке определенных объемов данных по заданному адресу в регламентируемое время с требуемым качеством.
СПД - большая система и характеризуется рядом внешних показателей. К их числу относится верность (достоверность) скорость и надежность.
Верность задается через допустимую вероятность ошибочного приема определенной порции данных. Чаще всего это ошибка приема байта. Типичное значение требуемой верности -10-6 на байт в банковских документах. В системах управления порцией служит команда (16-32 бита), а требование по допустимому значению ошибки более жесткое: 10-7 - 10-9 на команду.
Скорость подразумевают обычно относительную (0<R<1). Это коэффициент использования канала. Но задавать для проектирования величину R не всегда удается. Указывается чаще допустимая величина задержки и гарантируемая вероятность приема сообщения оговоренной длины с этой задержкой. По величине задержки различают СПД трех типов: реального времени (миллисекунды); запрос-ответ (секунды); некритичные к задержке (файловые). Скорость - одна из важнейших характеристик, т.к. в настоящее время стоимость передачи определяется в основном временем занятия канала.
Надежность - имеется в виду способность системы обеспечивать требуемое качество обмена (Pош, tзад, Pпр) в течение длительного времени.
Три указанные характеристики далеко не исчерпывающие. Стоимость - еще одна из очевидных внешних характеристик. В конкретных технических приложениях также могут быть такие характеристики как полоса канала, скрытность, энергопотребление, вес и т.д.
При системном подходе обеспечение внешних характеристик достигается за счет выбора внутренних параметров подсистем. Важнейшие внутренние параметры СПД - помехоустойчивость и пропускная способность системы. Помехоустойчивость оценивается вероятностью ошибки бита, а пропускная способность - числом бит в единицу времени, которые мы можем передать. Эти два параметра противоречивы.
Заданными являются при проектировании:
· ансамбль сообщений
· статистика ошибок (модель) канала
· набор внешних ограничений, как-то типы стыков, первичные коды, режим обмена (дуплекс-симплекс) и т.д
Система, гарантирующая требуемое качество передачи, называется допустимой. Основную трудность представляет поиск оптимальной системы. Оптимальность предполагает известным критерий. В качестве критерия часто используется одна из внешних характеристик. Скорость - наиболее употребляемый критерий, т.к. в основном она определяет цену и перспективу.
Конечная цель - найти систему, обеспечивающую передачу с требуемым качеством наиболее экономным способом. Минимизируют удельные затраты на передачу единицы информации (например на бит).
Проектирование СПД заключается в соответствующем выборе операторов, указанных в (*).
Математическое представление сигналов.
В зависимости от типа передаваемого сигнала, каналы подразделяются на непрерывные (аналоговые) и дискретные. В канале, непрерывном по амплитуде и во времени, сигнал может принимать в любой момент времени любое из непрерывного ряда значений (из бесконечно большого количества). В канале, дискретном во времени, сигнал может меняться лишь в определенные моменты времени, отстоящие друг от друга на интервал дискретизации. В большинстве случаев интервал дискретизации постоянен (на время работы), и можно говорить о периоде дискретизации и обратной величине - частоте дискретизации Fд. В чисто дискретном (цифровом) канале сигнал, дискретный во времени, может принимать одно из конечного множества состояний.
Дискретные сигналы представляют собой последовательности слов (которые не всегда являются числами); такая форма удобна и естественна для цифровых вычислительных систем.
Сигналы могут быть представлены в виде функций от времени s(t) либо функций от частоты. Представление в области времени вполне очевидно - это развертка значения (амплитуды) сигнала во времени, которое, например, можно наблюдать на осциллографе.
Пусть имеется функция времени S(t) на конечном интервале (t1, t2) и есть ортогональная система функций 
. Ортогональность означает, что: 
).
Утверждается, что
где 
.
Последнее означает, что функция, заданная на конечном временном интервале, представима в виде ряда по системе ортогональных функций. Если S(t) - периодическая, то она представима в виде ряда на всей оси времени.
Наиболее часто в качестве ортогональных функций берутся тригонометрические функции 
. Тогда получается тригонометрический ряд Фурье:
, 
, k=0,1,2
Если воспользоваться формулами Эйлера и перейти к комплексной переменной, то получим экспоненциальную форму ряда Фурье:
, 
, 
(формула Эйлера).
Набор коэффициентов ak, bk или 
k называют амплитудным спектром сигнала.
Большая часть реальных сигналов требует задания на бесконечном промежутке времени и не является периодическими. Чтобы представить такие сигналы используются прямое и обратное преобразование Фурье или спектральную плотность:
- спектр функции (t) или прямое преобразование Фурье.
- обратное преобразование Фурье.
Для расчета спектра функционально связанных сигналов полезно использовать ряд свойств. Перечислим их без доказательств. Будем обозначать символически прямое преобразование Фурье как F {v(t)}, а обратное F-1 {V(
)}.
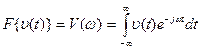
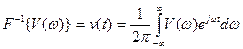
1. Свойство изменения масштаба
, a – действительное число
2. Свойство линейности
3. Свойство симметрии
4. Свойство запаздывания
5. Теорема модуляции
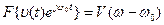
6. Свойство дифференцирования
или 
7. Свойство интегрирования
8. Теорема о спектре свертке функций
9. Теорема о спектре произведения функций
10. Теорема Рэлея (энергия сигнала равна энергии спектра)
Для существования преобразования Фурье требуется абсолютная интегрируемость функций, т.е. 
. Широко распространенные модели сигналов в радиотехнике такие как единичный скачок u(t), гармоничное колебание 
не обладают свойством абсолютной интегрированности, и в строгом смысле не имеют преобразования Фурье. Чтобы эту трудность обойти прибегают к искусственному приему. Один из способов преодолеть эту трудность сводится к введению несколько необычной функции Дирака или 
- функции (единичный импульс) – другое ее наименование.
Определим эту функцию, задав ее свойства:
1. 
2. 
- симметричность (четная относительно t0)
3. 
, т.е. 
4. 
- фильтрующее свойство.
Физически эту функцию можно представить себе как предельную последовательность обычных функций. Например, прямоугольных импульсов, имеющих площадь равную единице, когда 
.
Можно взять и функцию отсчетов 
, тогда
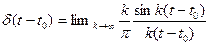
Обратное преобразование определим формально – это - функция.
Стробирующая функция
 |
Преобразование Фурье от постоянной составляющей (t)=A найдем как предел стробирующей функции с амплитудой А при 
.
Гармонический сигнал
Единичный скачок
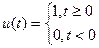
Представим u(t) в виде 
.
Вычтем среднее значение 
, получим
.
Согласно теореме интегрированности по времени
, т.е.
Третий способ математического задания сигналов, который принципиально важен и позволяет рассматривать передачу любого сообщения и дискретного и непрерывного с единой позиции как передачу чисел (данных), основан на теореме Котельникова.
Формулировка теоремы Котельникова следующая: Если непрерывная функция времени имеет спектр, ограниченный полосой частот от 0 до F Гц, удовлетворяет условиям Дирихле, то она полностью определяется своими мгновенными значениями, отстоящими друг от друга на 1/F с.
Теорема устанавливает возможность полного восстановления детерминированного сигнала с ограниченным спектром по его отсчетам и указывает предельное значение времени между отсчетами, при котором такое восстановление еще возможно. Непрерывный сигнал, таким образом, может быть задан в цифровой форме в виде последовательности мгновенных значений.
