При t→ ∞, 
, т.е 
. Из начальных условий определим А.
, поэтому из условия 
,
получим 
Таким образом, при t≥0:
и 
. (6)
Видно что 
нарастает по экспоненциальному закону, стремясь к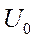 
. Скорость нарастания зависит от 
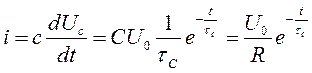(7)
Ток, определяемый выражением (7), убывает по экспоненте.
Аналогично изменяется напряжение на сопротивлении:
Во время переходного процесса в емкости накапливается электрическая энергия. При t→ ∞
Одновременно часть энергии, отдаваемой источником, расходуется в активном сопротивлении. Энергия теряемая и накапливаемая равны 
4.2) Включение в цепь RC гармонического напряжения.
Пусть при t≥0: 
.
Решение 
. Найдем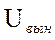 
.
Ток в цепи 
Напряжение на емкости отстает по фазе от тока на 90º. Поэтому вынужденное напряжение на конденсаторе:
где 
.
Напряжение на конденсаторе 
имеет вынужденную и свободную составляющие:
Определим А из начальных условий. Так как при t=(0+), 
=0, то
Следовательно, напряжение на конденсаторе во время переходного процесса при воздействии на цепь гармонического изменяющегося напряжения равно:
Характер изменения 
зависит от соотношений 
и 
.
1.б) пусть в момент включения источника мгновенное значение напряжения на емкость равно 0.
Это имеет место при 
. При этом собственных процессов не возникает, в цепи сразу устанавливается стационарный режим:
,
где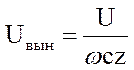 
2.б) в общем случае 
, тогда 
существенно отличается от напряжения вынужденных колебаний. Так при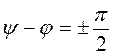 
, имеем (при большом τс , τс >>Т) напряжение 
изменяется по закону 
, но относительно кривой 
.
4.3)Разряд конденсатора на сопротивление.
Пусть в цепи RC с заряженным конденсатором С установливается режим короткого замыкания.
Так как при t>0 внешнего воздействия нет, то в цепи будут только собственный процесс (т.е. свободный режим). Поэтому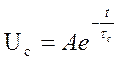 
. Определим А.
Так как конденсатор был заряжен, то в момент t=(0+) 
, тогда 
, А=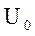 
.
Окончательно получим: 
.
Ток разряда
«-» ─ направление тока противоположно току заряда. Закон изменения 
и 
─ экспоненциальный.
При разряде электрическая энергия конденсатора расходуется в виде тепловых потерь на сопротивлении.
ВЫВОДЫ
1) Переходные процессы в цепях описываются дифференциальными уравнениями. Порядок дифференциальных уравнений определяется количеством реактивных элементов L и C.
2) Классический метод решений дифференциальных уравнений. Переходный процесс складывается из свободной (или переходящей, временной) составляющей и вынужденной составляющей. Свободная составляющая зависит от типа цепи и для рассмотренных цепей имеет вид 
(или 
). Вынужденная составляющая зависит от вида воздействия и представляет собой электрическую величину (i или u) в установившемся режиме.
Цепь RC:
а) Реакция на скачок: iв= I0, iсв =-I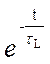 
.
б) При синусоиде: 
, 
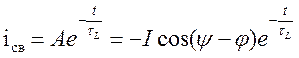
ЦЕПЬ RL:
а) Реакция на скачок: 
, 
б) При синусоиде: 
, 
(зависимость от угла как в цепи RL, только с противоположным знаком).
3) Законы изменения i, UR, UL, UC ─ экспоненциальные при скачках входного напряжения.
4) При синусоидальном воздействии переходной процесс имеет адиттивный характер: гармонический процесс (вынужденная составляющая) накладывается на собственный процесс; если собственная составляющая равна 0, то имеет место только установившейся режим.
5) При разряде L или C энергия магнитного или электрического поля расходуется в виде тепла на сопротивление R.
Общая схема применения классического метода анализа переходных процессов.
1) Сначала проводят анализ цепи до коммутации ─ определяют токи индуктивностей и напряжения на емкостях в момент времени, непосредственно перед коммутацией (t=0-).
2) Определение независимых начальных условий ─ токи индуктивностей (iL)и напряжения на емкостях (UC) в момент t=(0+) находят с помощью законов коммутации.
3) Составление дифференциального уравнения цепи после коммутации (при 
). Получают из системы уравнений для цепи (1-й и 2-й законы Кирхгофа) путем исключения всех переменных, кроме искомой.
4) Анализ установившегося процесса в цепи после коммутации (при 
) ─ находят вынужденную составляющую реакцию цепи (для искомой величины).
5) Определение свободной составляющей искомой величины (реакции цепи) ─ решение однородного дифференциального уравнения: составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи.
6) Нахождение общего вида реакций цепи ─путём суммирования свободной и вынужденной составляющих.
7) Определение постоянных интегрирования ─ по начальным условиям, в начальный момент после коммутации.
8) Определение реакции цепи, соответствующей заданным начальным условиям ─ подставить постоянные интегрирования в общее решение дифференциального уравнения.
