ПРЕДИСЛОВИЕ
Целью изучения данной дисциплины является знакомство студентов с основными понятиями и методами линейной алгебры, формирование у студентов научного математического мышления, умения применять математический аппарат для исследования экономических процессов.
В курсе данной дисциплины студенты овладевают знаниями по таким разделам линейной алгебры, как алгебра матриц, системы линейных уравнений. В процессе обучения происходит приобретение практических навыков решения типовых задач, способствующих усвоению основных понятий в их взаимной связи, а также задач, способствующих развитию начальных навыков научного исследования.
Учебная дисциплина «Линейная алгебра» входит в базовую часть дисциплин естественнонаучного цикла; требования к входным знаниям и умениям студента – знания, полученные в рамках школьного курса математики, и основы математического анализа. Данная дисциплина является предшествующей для следующих дисциплин: теория вероятностей и математическая статистика, методы оптимальных решений, эконометрика, статистика, макроэкономика, макроэкономическое планирование и прогнозирование.
В результате освоения дисциплины студент должен:
знать:
- основы векторной алгебры;
- математические операции над матрицами;
- способы вычисления определителей;
- методы решения систем линейных уравнений;
- метод определения собственных значений и собственных векторов матриц;
- алгоритм приведения квадратичных форм к суме квадратов.
уметь:
- производить основные операции над матрицами и векторами;
- находить определители матриц;
- проводить анализ систем линейных уравнений на наличие решений;
- решать системы линейных уравнений разными методами;
- находить собственные значения и собственные векторы матриц;
- работать с квадратичными формами;
- анализировать и идентифицировать исследуемые прикладные задачи;
- осуществлять выбор адекватных методов решения поставленных задач;
- использовать полученные знания для осуществления анализа экономических ситуаций.
владеть:
- навыками решения задачи и интерпретации результатов в терминах прикладной области;
- навыками применения компьютерных технологий реализации методов линейной алгебры.
ТЕМА 1.МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:
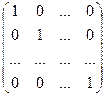 = E,
= E,
называется единичной матрицей.
Определение. Если amn = anm, то матрица называется симметрической.
Пример.  - симметрическая матрица
- симметрическая матрица
Определение. Квадратная матрица вида  называется диагональной матрицей.
называется диагональной матрицей.
ОСНОВНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ И ИХ СВОЙСТВА
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример. Даны матрицы А =  ; B =
; B =  , найти 2А + В.
, найти 2А + В.
2А =  , 2А + В =
, 2А + В =  .
.
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
 A×B = C;
A×B = C;
 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.






