Сигнал ошибки 
можно представить как сумму среднего значения 
и некоторой центрированной случайной составляющей 
:
.
Первое слагаемое представляет так называемую дискриминационную характеристику, определяющую зависимость среднего значения сигнала ошибки от рассогласования. Второе слагаемое связано с так называемой флуктуационной характеристикой 
, определяющей зависимость спектральной плотности сигнала ошибки от рассогласования.
Для последующего анализа указанных (дискриминационной и флуктуационной) характеристик дискриминатора определим взаимную корреляционную функцию колебаний на выходе двух каналов, формирующих корреляционные интегралы с расстройкой по измеряемому параметру;
где 
- удвоенная мощность накопленного шума;
- нормированная корреляционная функция накопленного шума;
- нормированная корреляционная функция когерентно накопленного сигнала,
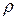- отношение сигнал-шум по мощности после когерентного накопления сигнала;
- функция рассогласования с гауссовой аппроксимацией, характеризующая критичность корреляционной обработки к расстройке опорного сигнала по измеряемому параметру (рис. 16.4);
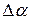- разрешающая способность по измеряемому параметру 
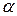, определяющая эффективную ширину функции рассогласования. Заметим, что аппроксимация функции рассогласования гауссовой кривой для произвольного измеряемого параметра способствует аналитичности решения последующих задач и сохранению основных закономерностей, лежащих в основе измерений.
Рис. 16.4. Функция рассогласования по измеряемому параметру
Будем рассматривать не частный случай "точечного" объекта наблюдения (цели), а общий случай "протяженного" объекта наблюдения (цели), когда диапазон блужданий энергетического центра отражения, излучения, рассеяния, распространения радиоволн по измеряемой координате 
, вызванных "шумами" цели ("шум дальности", "доплеровский шум", "угловой шум"), является не пренебрежимо малым, а становится соизмеримым с разрешающей способностью по измеряемой координате (параметру) 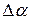. Будем полагать "шумы" цели нормально распределенными, а плотность вероятности измеряемой координаты (параметра) цели будем описывать гауссовой кривой (рис. 16.5):
,
где 
- центр блуждания параметра 
; 
- среднее квадратичное значение блужданий параметра ; 
- эффективный диапазон блужданий параметра .
Рис. 16.5. Плотность вероятности «шумов» объекта наблюдения (цели)
Усредненное по "шумам" цели произведение функций рассогласования, входящее в выражение для 
, принимает следующий вид:
где 
- радикал, определяющийся соотношением диапазона блужданий и разрешающей способности 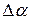по измеряемому параметру;
- каноническая форма функции рассогласования.
При этом усредненная по "шумам" цели взаимная корреляционная функция колебаний на выходах расстроенных по измеряемому параметру каналов
В частности, средний квадрат обобщенного корреляционного интеграла, следующий из последнего выражения при 
и 
, имеет вид
.
На рис. 16.6 показана зависимость его нормированного по шуму значения от рассогласования 
;
.
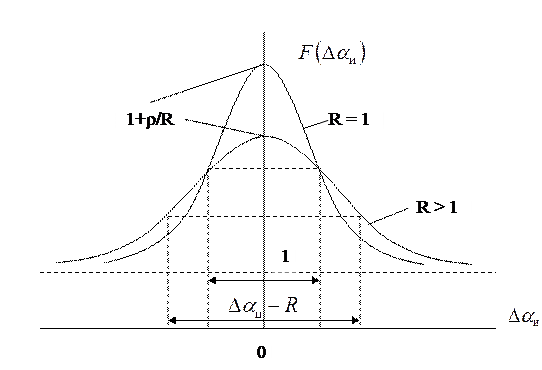
Рис. 16.6. Зависимость нормированной по шуму мощности выходного колебания коррелятора от рассогласования с учетом «шумов» цели
Из рисунка следует, что под действием "шумов" цели происходит "размывание" функции рассогласования, т.е. ее расширение в R раз, а также уменьшение усредненного по "шумам" цели произведения функций рассогласования в R раз.
Полученное выражение для среднего квадрата модуля обобщенного корреляционного интеграла, позволяет определить дискриминационную характеристику, т.е. зависимость среднего значения сигнала ошибки на выходе дискриминатора от рассогласования (рис. 16.7):
,
а также крутизну дискриминационной характеристики
, где 
.
Рис. 16.7. Вид дискриминационной характеристики
Таким образом, крутизна дискриминационной характеристики максимальна (по модулю) для "точечного" объекта наблюдения
, 
и уменьшается по мере увеличения относительной "протяженности" цели 
. Например, для "умеренно протяженной" цели 
крутизна дискриминационной характеристики уменьшается из-за "шумов" цели по сравнению с максимальной в 
раз, т.е., примерно в 5 раз.
Заметим, что в квазиоптимальных дискриминаторах существует оптимальное значение расстройки 
, соответствующее максимальной крутизне дискриминационной характеристики. Действительно, дискриминационная характеристика в этом случае согласно алгоритму формирования сигнала ошибки [см. п. 16.2] пропорциональна разности квадратов смешенных функций рассогласования
,
а крутизна дискриминационной характеристики оказывается зависимой от расстройки:
.
Исследуя эту зависимость на экстремум при гауссовой аппроксимации функции рассогласования, можно найти оптимальное значение расстройки , при котором крутизна дискриминационной характеристики квазиоптимальных дискриминаторов максимальна:
.
