Охарактеризуйте зонную схему кристаллических тел, полупроводников, проводников, диэлектриков. ХУЙ
Получите зависимость концентрации свободных носителей в полупроводнике от положения уровня Ферми.
В отличие от металлов, в которых электронных газ является вырожденным и подчиняется статистике Ферми-Дирана, в собственных и слаболегированных примесных полупроводниках электронный (дырочный) газ является невырожденным и распределение электронов по состояниям описывается классической статистикой Максвелла-Больцмана. Для таких полупроводников концентрация свободных носителей зависит от положения уровня Ферми и температуры Т. При температуре отличной от нуля в зоне проводимости полупроводника находятся электроны и в валентной зоне дырки. Обозначим их концентрацию через n и р.
Определим равновесную концентрацию электронов проводимости в зоне проводимости. При этом за нулевой уровень отсчета энергии электронов принимается потолок валентной зоны.
Концентрацию электронов, энергия которых заключена в интервале от Е до E+dE можно выразить следующим образом dn=Nn(E)*2fM-БdE, (2.2.1)
где Nn(E) - число элементарных фазовых ячеек или состояний, приходящихся на единичный интервал энергии; fM-Б - функция распределения Максвелл-Больцмана,
fM-Б 
, выражающая вероятность заполнения электроном с энергией Е фазовой ячейки.
Множитель 2 выражает принцип Паули.Как нам известно 
Тогда (2.2.1) можно записать в виде 
. (2.2.2)
Полное число электронов n, находящихся при температуре Т в зоне проводимости, можно получить интегрируя (2.2.2) по всем значениям энергии соответствующим зоне проводимости 
.(2.2.3)
Проинтегрировав (2.2.3) получим 
.(2.2.4)
Если провести подобный расчет для дырок, то можно получить аналогичное выражение 
.(2.2.5)
В (2.2.4) и (2.2.5) mn и mp эффективные массы дырок и электронов.
Из выражений (2.2.4) и (2.2.5) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми EF, чем больше это расстояние, тем ниже концентрация носителей.
Произведение n на р для любого невырожденного полупроводника равно: 
.(2.2.6)
Это формула показывает, что при фиксированной температуре произведение концентраций электронов и дырок для данного полупроводника является величиной постоянной. Соотношение (2.2.6) выражает так называемый закон действующих масс в применении к газу свободных носителей в полупроводниках.
Охарактеризуйте положение уровня Ферми и концентрацию носителей в собственных полупроводниках.
Если в полупроводнике нет примесей, так что NA=ND=0, где NA и ND - концентрации соответственно акцепторной и донорной примесей, то такой полупроводник называется собственным или чистым. В собственных полупроводниках концентрация электронов в зоне проводимости ni равна концентрации дырок в валентной зоне pi.i=p (2.3.1) Индексами «i» обозначают равновесные концентрации в собственных полупроводниках. Приравнивая правые части соотношений (2.2.4) и (2.2.5) получаем
, 
,откуда 
. (2.3.2)
Это соотношение определяет положение уровня Ферми в собственных полупроводниках. При абсолютном нуле Т=0: 
,(2.3.3)
где Eg - ширина запрещенной зоны. Т.е. при Т=0 уровень Ферми располагается посередине запрещенной зоны.
С повышением температуры он смещается вверх к дну зоны проводимости, если mp>mn и вниз если mp<mn (рис. 2.4). Однако, в большинстве случаев это смещение настолько незначительно, что им можно пренебречь и считать, что уровень Ферми в собственных полупроводниках располагается по середине зоны.
Если подставить EF из (2.3.3) в (2.2.4) и (2.2.5), то получим 
. (2.3.4)
Из (2.3.4) следует, что равновесная концентрация носителей заряда в собственном полупроводнике определяется шириной запрещенной зоны Eg. При чем зависимость ni от T и Eg очень сильная.
Из (2.3.4) можно получить: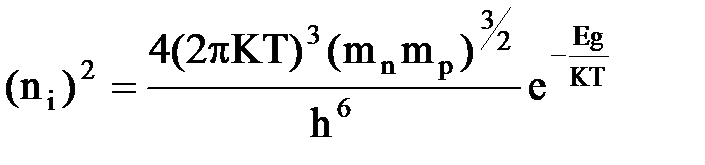 
. (2.3.5)
Правые части (2.3.5) и (2.2.6) равны, следовательно, равны и левые
. (2.3.6)
Это выражение также выражает закон действующих масс. Из (2.3.6) следует, что концентрация электронов и дырок в любом невырожденном полупроводнике таковы, что их произведение равно квадрату собственной концентрации электронов. Соотношение (2.3.6) справедливо при любой температуре
. (2.3.7)
