Когда известны индексы кристаллографических плоскостей параметры решетки можно определить следующим способом. Перепишем уравнение (8), выполнив замену переменных следующим образом:
h2A+k2B+l2C+hkD+hlE+klF = Qjhkl, j = 1, …,N; (9)
где: A=a*2, B=b*2, C=c*2, D=2a*b*cosg*, E=2a*c*cosb*, F=2b*c*cosa*, Qjhkl=1/dj2hkl,, djhkl, - экспериментальное межплоскостное расстояние, определенное по формуле Вульфа-Брэгга из позиции j- й линии 2Qj рентгенограммы, N – количество линий.
В результате получили систему (9) из N уравнений c целочисленными коэффициентами, линейных относительно шести неизвестных A,B,C,D,E,F. Чтобы найти эти параметры, необходимо и достаточно выбрать шесть независимых линий с известными индексами и позволяющих решить систему уравнений, которая будет определена и имеет единственное решение. На практике число линий рентгенограммы больше шести, что даёт возможность контролировать достоверность результатов. В этом случае, вместо однозначно решаемой системы получается переопределённая система, которая в общем случае не имеет решения. Метод наименьших квадратов (МНК) позволяет перейти от N условных уравнений к 6-ти нормальным уравнениям путём минимизации функционала, составленного из суммы квадратов ошибок между левыми и правыми частями системы уравнений (9).
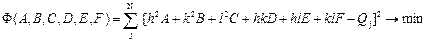Функционал должен сходится к минимуму при истинных значениях параметров a,b,c,a,b,g. Минимизация функционала МНК производится путем его дифференцирования по неизвестным, при этом каждая частная производная должна обращаться в нуль в точке экстремума (минимума):
(10)
Таким образом, получена система из шести нормальных уравнений с 6-ю неизвестными, которую можно решить, например, по методу Гаусса, затем вычислить значения параметров обратной решетки a*,b*,c*,a*,b*,g* и, далее, по формулам (7), значения параметров прямой решетки a,b,c,a,b,g. Система нормальных уравнений (10) даёт единственное решение, которое является наиболее вероятным для системы условных уравнений (9). Для этого необходимо 2 условия: во-первых, каждой экспериментальной линии рентгенограммы должны быть правильно присвоены кристаллографические индексы, во-вторых, позиции экспериментальных линий должны быть определены с высокой точностью.
Высокой точности определения периодов (с погрешностью 0,001-0,0001 ангстрем и лучше) можно достигнуть, применяя особые методы съемки и обработки результатов измерения рентгенограмм, так называемые прецизионные методы. Достижение максимальной точности в определении периодов решетки возможно следующими методами:
1) использование значений межплоскостных расстояний, определенных из углов в прецизионной области;
2) уменьшение погрешности в результате точной настройки дифрактометра и увеличения экспозиции съемки рентгенограммы;
3) использование методов графической или аналитической экстраполяции.
Минимальная погрешность Dd/d получается при измерениях в районе углов 2q ~150¸1700. К сожалению, далеко не все вещества дают на рентгенограмме линии под такими большими углами. В этом случае для измерений следует использовать линию под возможно большим углом 2q. Увеличение точности определения параметров ячейки связано также с уменьшением случайных ошибок, которые можно учесть только усреднением, и с учетом систематических погрешностей, если известны причины их возникновения.
Учет систематических погрешностей при определении параметров решетки сводится к нахождению зависимости систематических погрешностей от брэгговского угла q, что позволяет провести экстраполяцию к углам q = 900 (2q = 1800), при которых погрешность определения межплоскостных расстояний становится малой. К случайным погрешностям относятся погрешности измерения, связанные с определением положения дифракционной линии на рентгенограмме. К систематическим относятся погрешности, обусловленные геометрией съемки и физическими факторами.
