Пусть генеральные совместимости 
, m1, m2 известны. 
- выборки из X и Y соответственно.
Найдем закон распределения отношения выборки дисперсий 
распределение Фишера
Т.о.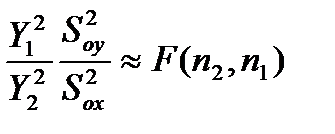 
Интервальные оценки. Доверительный интервал. Доверительная вероятность.
В ряде задач требуется не только найти для параметра 
подходящую оценку 
, но и указать к каким ошибкам может привести замена параметра 
его оценкой 
, т.е. требуется оценить точность и надежность оценки.
Для определения точности оценки 
в статистике пользуются доверительными интервалами.
Для определения надежности оценки 
в статистике пользуются доверительной вероятностью.
Опр. Доверительным интервалом для параметра 
называется интервал 
, содержащий истинное значение параметра с заданной вероятностью 
.
.
Опр. Число называется доверительной вероятностью, а значение a – уровнем значимости.
Замечание. Нижняя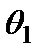 
и верхняя 
граница доверительного интервала определяется по результатам наблюдений и следовательно является СВ. Поэтому так и говорят, что доверительный интервал «накрывает» оцениваемый параметр с вероятностью 
.
Выбор доверительной вероятности каждый раз определяется конкретной постановкой задачи. Обычно р = 0,9; р = 0,95; р = 0,99.
Часто применяют односторонние доверительные интервалы
(левосторонний), 
(правосторонний).
В простейших случаях метод построения доверительных интервалов состоит в следующем 
–оценка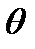 
, 
. Предположим, что существует непрерывная и монотонная функция Y, зависящая от 
и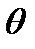 
, но такая, что ее распределение не зависит от 
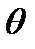и других параметров. Для нахождения границ доверительного интервала 
по заданной доверительной вероятности . В этом случае можно использовать неравенство 
, где числа 
, определяются из условия
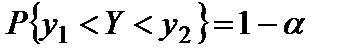
Рассмотрим нахождение доверительного интервала для среднего и дисперсии нормально распределенной генеральной совокупности.
Доверительный интервал для оценки МО при НЕизвестной дисперсии
2)Доверительный интервал для оценки МО при неизвестной дисперсии нормально распределенной генеральной совокупности. Пусть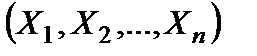 
– выборочный вектор n –наблюдений СВ 
. В качестве оценки для m возьмем 
. Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику 
. Доверительный интервал для m в этом случае находится с помощью статистики 
.
В литературе по статистике показано, что Y имеет распределение Стьюдента с n –1 степенью свободы 
.
По заданной доверительной вероятности 
, используя таблицы распределения Стьюдента с n –1 степенью свободы, находим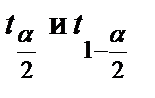 
.
.
.
.
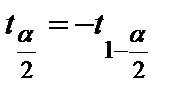
