1. Квадратные уравнения.
1.1. Приведём более простой по сравнению с учебником способ вывода формулы корней квадратного уравнения.
Рассмотрим квадратное уравнение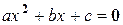 
, где а ¹ 0.
Умножим обе части уравнения на 4 а, получим уравнение 
, равносильное данному по свойству 2.
Выделим полный квадрат 
, 
.
Введём обозначение 
и назовём полученное выражение дискриминантом (в переводе «различитель»). Уравнение примет вид 
.
Рассмотрим 3 случая.
1случай. 2случай 3 случай.
D>0. D=0. D<0.
Тогда 
, 
Корней нет.
Делаем вывод о количестве корней уравнения. Авторы учебника [2] считают, что во втором случае уравнение имеет один корень. Их точка зрения понятна, если исходить из того, что решить уравнение – это значит найти множество его корней. Тогда запись { 
, } - безграмотна. С другой стороны, основная теорема алгебры утверждает, что уравнение имеет столько корней, какова его степень. Значит, квадратное уравнение имеет в этом случае два корня. В высшей алгебре вводится понятие кратного корня. Поэтому можно сказать, что корень один, но кратность его равна 2. В школьном курсе понятие кратности корня не используется, поэтому говорят, что уравнение имеет два равных корня.
1.2. Следует добиться знания всеми учащимися формулы корней квадратного уравнения 
со вторым чётным коэффициентом:
.
1.3. Важным средством проверки правильности решения квадратного уравнения служит теорема Виета, а обратная теорема позволяет устно найти корни квадратного уравнения. Поэтому следует настойчиво формировать умение учащихся применять эти теоремы.
1.4. Иногда рассматривается формула корней приведённого квадратного уравнения 
: 
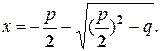Для запоминания формулы Радионяня сочинила стишок:
Чтобы решить уравненье,
Корни его посчитать,
Нужно немного терпенья
Ручка, перо и тетрадь.
Минус напишем сначала,
Рядом с ним р пополам,
Плюс, минус знак радикала,
С детства знакомого нам.
Ну а под корнем, приятель,
Сводится всё к пустяку:
р пополам и в квадрате,
Минус несчастное q.
Старомодно, но запомнить помогает.
2. Дробные рациональные уравнения.
Существуют различные методы решения дробных рациональных уравнений. Один из них состоит в приведении такого уравнения к виду 
, затем используется условие дроби равенства нулю, позволяющее получить равносильную данному уравнению систему 
Учителя, работающие в школе, когда в учебнике приводилось такое решение, до сих пор предпочитаю пользоваться таким методом. Авторы современных учебников предлагают решать дробно – рациональные уравнения методом приведения к целому виду. Однако, ввиду того, что теория равносильности в школе не рассматривается, такой метод нельзя считать теоретически обоснованным.
На примере решения уравнения 
формулируется алгоритм:
1) найти общий знаменатель дробей, входящих в уравнение;
2) умножить обе части уравнения на общий знаменатель;
3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Для обоснования приведённого алгоритма, используется свойство об умножении обеих частей уравнения на число, отличное от нуля. С оговоркой «мы умножали обе части не на число, отличное от нуля, а на выражение, содержащее переменную, которое может обращаться в нуль. Поэтому не каждый корень полученного целого уравнения обязательно окажется корнем данного уравнения». Приведённые рассуждения и делают необходимым пункт 4 приведённого алгоритма.
Методические аспекты изучения уравнений других видов будут рассмотрены в дальнейшем, при обсуждении методики изучения тригонометрии, показательной, логарифмической функции. Математические аспекты линии уравнений и неравенств достаточно полно представлены в курсах «Введение в математику» (6 семестр) и «Элементарная математика» (8 семестр).
