Движение точки может быть задано зависимостями ее координат (
от времени (
), т.е. 
, 
, 
или же если траектория точки известна, зависимостью, зависимостью дуговой координаты (
) от времени, т.е. 
(см. рисунок 22).
В первом случае скорость (
) и ускорение (
) точки определяются через свои проекции на оси декартовой системы координат:
для скорости – проекция скорости на ось равна производной по времени от соответствующей координаты, выраженной зависимостью (функцией) от времени (). Проекции 
скорости точки на оси 
, 
, 
соответственно, находятся по формулам:
; 
; 
;
для ускорения – проекция ускорения на ось равна производной по времени от соответствующей проекции скорости. Проекции 
ускорения точки на оси , , соответственно, находят по формулам:
; 
; 
.
Модули скорости 
и ускорения 
точки находятся так:
.
В том случае, если траектория точки и ее дуговая координата заданы, скорость точки направляется по касательной к траектории в сторону увеличения координаты и находится производной по времени от дуговой координаты, выраженной функцией от времени 
.
Ускорение точки находится через две составляющие 
и 
, т.е. 
и 
.
Составляющая называется нормальным ускорением, направляется по нормали к траектории точки (перпендикулярно касательной) и равна:
где 
- радиус траектории в данной точке.
Составляющая называется касательным ускорением, направляется по касательной к траектории (т.е. перпендикулярно ) и равна второй производной по времени от дуговой координаты:
Модуль 
может быть найден и через проекции на координатные оси , , скорости и ускорения точки т.е.
При сложном движении точки (т.М), ее скорость (абсолютная скорость 
) определяется по формуле:
(17)
где: 
- переносная скорость точки, или скорость точки тела, с которой, двигаясь по этому телу со скоростью 
, совпала рассматриваемая точка (т.М); - относительная скорость точки М (см. рисунок 23).
Ускорение точки при сложном движении точки (абсолютное ускорение 
) определяется геометрической суммой трех ускорений 
:
, (18)
где 
– переносное ускорение точки, или ускорение точки тела, с которой, двигаясь по этому телу с ускорением , совпала рассматриваемая точка М; 
– относительное ускорение точки М; 
- кориолисово ускорение т. М, оно равно
и направлено перпендикулярно плоскости, в которой лежат векторы угловой скорости 
переносного движения (направлен по оси вращения тела) и относительной скорости точки.
Численные значения абсолютных скорости и ускорения точки определяются из скалярных уравнений, которые получаем, спроектировав векторные уравнения (17) и (18) на оси координат , .
Вращательное движение тела задается зависимостью угла 
поворота тела от времени:
и характеризуется угловыми скоростью 
и ускорением 
.
Угловая скорость тела определяется первой производной по времени от угла поворота:
Угловое ускорение тела равно первой производной по времени от угловой скорости, выраженной зависимостью от времени:
При равномерном (
вращении тела угол поворота тела имеет следующую зависимость от времени (
: 
.
Быстрота вращения тела характеризуется не только угловой скоростью (рад/с), но частотой вращения 
(об/мин), их связь определяется формулой
где число 
можно взять равным 3,14.
При равнопеременном (
вращении тела угол зависит от времени ( так
,
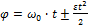где 
- угловая скорость в начальный момент времени.
Угловая скорость тела в этом случае определяется формулой
.
В приведенных выше формулах знак “+” перед берется при ускоренном вращении, знак “-” – при замедленном.
Скорость (
точки (т. М) тела при его вращательном движении направлена перпендикулярно кратчайшему расстоянию от точки до оси вращения тела (по касательной к траектории точки) в сторону вращения тела (по направлению угловой скорости ) и равна: 
, м/с, где 
- кратчайшее расстояние от точки до оси вращения тела (
см. рисунок 24).
Ускорение точки находится через нормальное 
, направленное по кратчайшему расстоянию к оси вращения тела, и касательное 
, направленное перпендикулярно нормальному в сторону углового ускорения тела. Величина ускорений , и определяются по формулам:
; 
; 
.
При плоскопараллельном (плоском) движении тела скорость точки тела можно найти тремя способами:
Первый способ, заключающийся в использовании общей формулы, покажем на следующем примере. Для четырехзвенного механизма ОАВС, находящегося в данный момент времени в положении, указанном на рисунке 25, скорость точки В, если скорость т. А известна, находится по формуле:
,
где 
– скорость т. В в относительном вращении отрезка ВА вокруг точки А с угловой скоростью 
(
.
Второй способ основан на теореме о проекциях скоростей: при плоском движении тела, проекции скоростей двух его точек на линию, соединяющую точки, равны (см. рисунок 26): 
. Скорость точки А легче вычислить если известна скорость точки А и можно найти углы 
и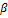 
.
В третьем способе для определения скорости используется мгновенный центр скоростей точек (лежит на пересечении перпендикуляров к векторам скоростей). Скорости точек прямо пропорциональны их расстояниям до мгновенного центра скоростей:
Для определения ускорения точки при плоском движении тела используется общая формула, если известно ускорение одной точки тела и угловые скорость и ускорение относительного вращения тела вокруг этой точки:
, (
где 
, 
- нормальное и касательное ускорения т. В относительно т. А, их направление показано на рисунке 27, а модули находятся так:
; 
.
Векторные уравнения ( в проекции на оси 
дает два скалярных уравнения, решая которые определяем величину и направление ускорения т. В.
Задача 4. (К1). Тема: Кинематика точки.
Задание: Движение точки М задано координатным способом (зависимость ее координат и от времени дана в таблице 4). Определить: уравнение траектории точки в координатной форме, направление движения точки, а также в момент времени 
- положение, скорость, ускорение и радиус кривизны траектории точки.
Таблица 4
| Вариант | ,
м
| 
м
|
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
|
| |
| 
| |
|
|
| |
| 
|
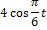
Порядок решения задачи покажем на следующем примере:
Дано:
___________________________
; 
; 
.
1.Запишем уравнение траектории точки М в координатной форме, исключив из уравнения ее движения время. Наличие в уравнениях тригонометрических функций позволяет использовать для этого формулы их соотношения: 
В нашем примере
по формуле 
получим:
после преобразования имеем:
Это уравнение параболы. Значит траектория точки М – парабола (она показана на рисунке 28).
2. Для того чтобы определить направление движения точки, необходимо найти ее координаты в момент времени 
и следующий момент времени (например 
).
При 
; 
.
При 
; 
.
Направление движения указано на рисунке 28.
3. Положение точки в момент времени 
определим, подставив в уравнение движения заданные значения времени (как в предыдущей точке).
При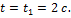 
.
Точка показана на рисунке.
4. Скорость точки найдем через ее проекции 
на оси координат.
,
,
При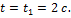
м/c;
м/с.
Модуль скорости равен
5. Ускорение точки найдем через ее проекции 
на оси координат.
,
,
При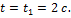
м/c2;
м/с2.
Модуль скорости равен
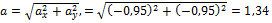м/с2.
6. Касательное ускорение точки найдем по формуле
при 
оно равно
м/с2.
Знак “-” в ответе показывает, что касательное ускорение направлено в сторону, противоположную скорости, т.е. движение точки в этот момент времени – замедленное.
7. Нормальное ускорение 
точки в момент времени равно
м/с2.
8. Радиус кривизны траектории точки в момент времени найдем из выражения
м.
Задача 5. (К2). Тема: Простейшие движения твердого тела. Сложное движение точки.
Задание: Дан четырехзвенный шарнирно-рычажный механизм 
(рисунок 29), состоящий из трех подвижных звеньев 
(звено 1), 
(звено 2), 
(звено 3) и одного неподвижного (звено 4). В движение механизм приводится за счет вращения с постоянной скоростью 
звена 1. Звено 3 также совершает вращательное движение, звено 2 – плоскопараллельное. По звену 2 или 3 движется ползушка 5 с постоянной скоростью 
. Для положения механизма и ползушки, указанного на рисунке, определить абсолютные скорость и ускорение точки 
ползушки, а также угловые скорости 
и 
и угловые ускорения 
и 
, звеньев 2 и 3. Необходимые для расчетов параметры даны в таблице 5.
Таблица 5
| Вариант | ,
рад/с
| 
град.
| 
град.
|  ,
град.
| 
| 
| 
| 
|  ,
|
| 0,25 | 0,5 | 1,2 | 1,0 | ||||||
| 0,3 | 0,4 | 0,3 | 0,9 | ||||||
| 0,25 | 0,25 | 0,8 | 0,5 | ||||||
| 0,3 | 0,5 | 1,2 | 1,0 | ||||||
| 0,4 | 0,4 | 1,0 | 0,8 | ||||||
| 0,4 | 0,5 | 1,2 | 0,8 | ||||||
| 0,25 | 0,4 | 1,0 | 0,75 | ||||||
| 0,5 | 0,5 | 1,5 | 1,0 | ||||||
| 0,3 | 0,6 | 1,4 | 0,9 | ||||||
| 0,4 | 0,6 | 1,2 | 1,0 |
Порядок решения задачи покажем на следующем примере: дан механизм, имеющий следующие размеры:
Дано:
; 
; 
; 
;
; 
; 
; 
.
_____________________________________________________
1. Определим скорость точки 
.
.
Направлен вектор скорости 
перпендикулярно в сторону угловой скорости .
2. Найдем скорость точки В с использованием теоремы о проекциях скоростей, учитывая, что, вектор скорости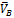 
должен быть перпендикулярен .
или
3. Угловую скорость звена 2 найдем через мгновенный центр 
скоростей этого звена.
расстояние 
найдем из треугольника 
по теореме синусов
или
Тогда
4. Определим угловую скорость звена 3.
Покажем дуговой стрелкой, направив ее в сторону, куда вектор 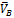поворачивает .
5. Вычислим переносную скорость точки М
где 
вектор скорости направлен перпендикулярно 
; в ту же сторону, что и вектор 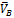(по направлению ).
6. Абсолютная скорость точки М равна
7. Найдем ускорение точки А, учитывая, что звено 1 (ОА) вращается с постоянной угловой скоростью
.
8. Касательное и нормальное ускорение т.В найдем, проецируя на оси 
векторное выражение
в проекции на ось
в проекции на ось
,
где 
.
Сначала из второго скалярного выражения находим 
:
Затем из первого скалярного выражения определяем 
.
Полное ускорение 
точки 
равно
.
9. Касательное 
и нормальное 
ускорения точки М найдем по формулам:
10. Найдем модуль кориолисово 
ускорения точки M
,
где 
; 
;
тогда 
.
Для определения направления ускорения повернем вектор на 
вокруг точки М по угловой скорости звена, на котором расположена ползушка.
11. Найдем переносное ускорение точки М через две составляющие: 
- нормальное и 
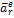- касательное, т.е.
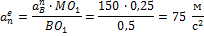
12. Абсолютное ускорение точки М определим спроецировав на оси 
и 
векторное уравнение:
.
Учитывая, что 
(так как 
получим
;
и модуль 
равен
.
13. Угловое ускорение звена 2 равно
14. Угловое ускорение звена 2 равно
ДИНАМИКА
