ВВЕДЕНИЕ
Методические указания предназначены для студентов заочного отделения института механизации и технического сервиса в целях закрепления и проверки знаний теоретической механики в объеме, определенной учебной программой.
Требования к оформлению контрольной работы.
Задачи по каждому разделу (статика, кинематика, динамика) решаются в отдельной тетради (двенадцатилистовой, в клетку). Решение задачи приводится в логической последовательности, с краткими поясняющими записями. Все записи, формулы, схемы должны быть сделаны аккуратно, ясно и четко. Текст контрольных работ выполняется черной пастой, рисунки – карандашом, все формулы должны быть пронумерованы (номер ставится в круглых скобках напротив формулы у правой границы листа).
Задание для выполнения контрольной работы берется по номеру зачетной книжки – предпоследняя цифра определяет номер рисунка, последняя – номер строки таблицы с данными.
СТАТИКА
Краткие сведения для решения задач
Сила – векторная величина, являющаяся количественной мерой взаимодействия двух тел.
Аксиома связи: Всякое несвободное тело можно представить свободным, если отбросить его связи, и их действие заменить реакциями.
Реакция связи направляется в сторону противоположную той, куда связь не дает перемещаться телу.
Реакции некоторых связей:
 1. Гибкая связь
1. Гибкая связь 
 2. Стержень
2. Стержень 

3. Гладкая поверхность 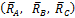
4. Подвижная шарнирная опора 

5. Ползун 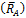

6. Неподвижная шарнирная опора 

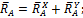
 .
.
7. Сферический шарнир 

Составляющие силы по осям и проекции ее на оси: Силы  и
и  - составляющие силы
- составляющие силы  по осям X и Y соответственно, а сила
по осям X и Y соответственно, а сила  в свою очередь – равнодействующая сил
в свою очередь – равнодействующая сил  и
и  (см. рисунок 8).
(см. рисунок 8).
 и
и 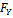 – проекции силы
– проекции силы  на оси
на оси 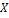 и
и  , соответственно.
, соответственно.

Проекция силы на ось – это скалярная величина, определяется отрезком оси, заключенной между двумя перпендикулярами к ней. Проекция силы на ось положительна, если ее составляющая по этой оси направлена в одну сторону с осью и отрицательна – если она направлена в сторону противоположную положительному направлению оси.
 т.к.
т.к.  направлена в сторону, противоположную оси
направлена в сторону, противоположную оси 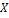 ,
,  так как
так как  и ось
и ось  направлены в одну сторону. Численные значения определяются по формулам
направлены в одну сторону. Численные значения определяются по формулам
 ,
,
 .
.
Алгебраическим моментом силы ( ) относительно точки (т. А) (для краткости слово “алгебраический ” в дальнейшем отбрасываем) называется взятое со знаком плюс или минус произведение модуля силы (
) относительно точки (т. А) (для краткости слово “алгебраический ” в дальнейшем отбрасываем) называется взятое со знаком плюс или минус произведение модуля силы ( ) на ее плечо (
) на ее плечо ( ) относительно точки.
) относительно точки.
 .
.
Плечом называется кратчайшее расстояние (перпендикуляр) от точки до линии действия силы.

Момент силы берется со знаком плюс (знак не пишется), если сила старается повернуть плечо вокруг точки против хода часовой стрелки и знаком минус, если – по ходу часовой стрелки.
Моментом силы ( ) относительно оси (оси
) относительно оси (оси  называется взятое со знаком плюс или минус произведение модуля проекции силы на плоскость перпендикулярную оси
называется взятое со знаком плюс или минус произведение модуля проекции силы на плоскость перпендикулярную оси  на плечо (
на плечо ( ) силы относительно оси (см. рисунок 10).
) силы относительно оси (см. рисунок 10).
 .
.

Знак плюс у момента берется, если при взгляде с положительного направления оси поворот силой плеча вокруг оси виден против хода часовой стрелки, знак минус – если по ходу.
Теорема Вариньона. Момент равнодействующей относительно точки или оси равен сумме моментов относительно точки и оси ее составляющих

Для точки
 ,
,
где  =
=  .
.
Для оси (см. рисунок 12):
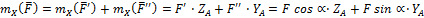 .
.

Для плоской системы произвольных сил можно составить три уравнения равновесия по трем условиям равновесия: указанная система сил будет находиться в равновесии, если сумма проекций сил на каждую из двух взаимно перпендикулярных осей (например, оси X и Y) равна нулю (т.е. 1.  2.
2.  ), а также равна нулю сумма моментов сил относительно произвольно взятой точки (3.
), а также равна нулю сумма моментов сил относительно произвольно взятой точки (3.  ).
).
Для пространственной системы произвольных сил можно составить шесть уравнений равновесия по шести условиям: указанная система сил будет находиться в равновесии, если сумма проекций сил на каждую из трех взаимно перпендикулярных осей равна нулю (1.  2.
2.  ) и сумма моментов сил относительно каждой из этих осей также равна нулю (4.
) и сумма моментов сил относительно каждой из этих осей также равна нулю (4.  ).
).
Задача 1 (С1). Тема: Равновесие плоской системы произвольных сил.
Задание. Дана Т-образная балка 
 , находятся в равновесии под действием сил
, находятся в равновесии под действием сил  ,
,  , пары сил с моментом
, пары сил с моментом  и распределенной силы интенсивности
и распределенной силы интенсивности 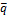 . Величины силовых нагрузок приведены в таблице 1. Балка удерживается в заданном на рисунке положении двумя опорами: неподвижной шарнирной опорой и подвижной шарнирной опорой или ползуном. Определить реакции опор (реакции связей).
. Величины силовых нагрузок приведены в таблице 1. Балка удерживается в заданном на рисунке положении двумя опорами: неподвижной шарнирной опорой и подвижной шарнирной опорой или ползуном. Определить реакции опор (реакции связей).
Алгоритм решения задач на равновесие системы сил (как плоской, так и пространственной).
1. Выбрать тело, равновесие которого надо рассмотреть (обычно это тело, к которому приложены заданные силы).
2. Показать на рисунке все заданные силы, приложенные к телу, при этом распределенные силы заменить сосредоточенными.
3. Установить связи тела и заменить их реакциями (представить тело свободным).
4. Составить необходимое количество уравнений равновесия системы сил, включающих в себя заданные силы, приложенные к телу и реакции его связей (количество уравнений зависит от вида системы сил).
5. Решить совместно полученные уравнения и определить искомые величины.
6. Проверить правильность результатов расчета.
Таблица 1
| Вари-ант |  ,
H ,
H
|  град.
град.
|  H
H
|  ,
град. ,
град.
| 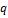 ,
H/м ,
H/м
| 

| 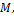

| 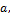

|
| 0,5 | ||||||||
| 0,6 | ||||||||
| 0,8 | ||||||||
| 0,4 | ||||||||
| 0,5 | ||||||||
| 0,6 | ||||||||
| 0,4 | ||||||||
| 0,8 | ||||||||
| 1,2 |



Рассмотрим порядок решения задачи на следующем примере: дана балка (см. рисунок 13), находящаяся в равновесии под действием заданных сил, численные значения которых и размеры балки приведены ниже. Определить реакции связей.
 Дано:
Дано:

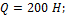
 ;
;

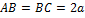 ;
;

 ;
;



1. Рассмотрим равновесие Т-образной балки  . Все заданные силы показаны на рисунке14. Распределенную силу заменим сосредоточенной силой
. Все заданные силы показаны на рисунке14. Распределенную силу заменим сосредоточенной силой  , приложенной в середине отрезка ДЕ (точке
, приложенной в середине отрезка ДЕ (точке  . Модуль силы
. Модуль силы  равен:
равен:
 .
.
2. Связи рассматриваемой балки: в точке  - неподвижная шарнирная опора, заменяем ее двумя составляющими
- неподвижная шарнирная опора, заменяем ее двумя составляющими  и
и  реакции
реакции 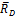 (
( ;
;  ; в точке
; в точке  – ползун, реакция связи
– ползун, реакция связи 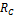 направлена перпендикулярно направляющим ползуна.
направлена перпендикулярно направляющим ползуна.

3. Система сил ( ), приложенных к балке является плоской системой произвольных сил. Для равновесия такой системы достаточно выполнения трех уравнений равновесия (неизвестных также три:
), приложенных к балке является плоской системой произвольных сил. Для равновесия такой системы достаточно выполнения трех уравнений равновесия (неизвестных также три:  ).
).
4. Составляем уравнения равновесия.
Сумма проекций сил системы на ось 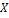 равняется нулю:
равняется нулю:
 (1)
(1)
Сумма проекций сил на ось  равняется нулю:
равняется нулю:
 (2)
(2)
Сумма моментов сил относительно точки  равняется нулю:
равняется нулю:
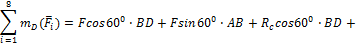

или

 (3)
(3)
5. Решаем совместно полученные уравнения:
Из (3):

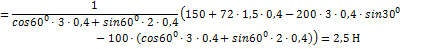
Из (2): 
= 
Из (1) 

6. Для проверки результатов расчетов, составим сумму моментов сил относительно точки  . Она должна равняться нулю.
. Она должна равняться нулю.



Ответ: 
Задача 2 (С2). Тема: Равновесие системы тел под действием произвольной плоской системы сил.
Задание. Дана система тел, состоящая из двух балок, соединённых между собой шарниром С. Она находится в равновесии под действием плоской произвольной системы сил, включающей в себя силы  , пару с моментом М (на рис. показана дуговой стрелкой) и распределённую силу, интенсивностью q. Все силовые по модулю и направлению известны, требуемые размеры балок указаны на рисунке. Определить реакции опор в точках А и В, а также шарнира С.
, пару с моментом М (на рис. показана дуговой стрелкой) и распределённую силу, интенсивностью q. Все силовые по модулю и направлению известны, требуемые размеры балок указаны на рисунке. Определить реакции опор в точках А и В, а также шарнира С.
Решение задачи на равновесие системы тел (механической системы) надо выполнять в следующем порядке:
1. Убедиться в статической определимости системы тел. Система статически определима, если количество неизвестных реакций связей не превышает количества уравнений равновесия, которые можно для неё составить.
2. Разбить систему (по соединяющим шарнирам) на отдельные тела, показав на расчётной схеме каждого из тел, приложенные к нему активные силы и реакции отброшенных связей.
3. Рассмотреть равновесие каждого тела в отдельности, определив тип действующей на него системы сил (активных сил т реакций связей) и составив в зависимости от этого необходимое количество уравнений равновесия.
4. Решить совместно уравнения равновесия всех тел системы и определить искомые величины.
5. Проверить полученные результаты.
Таблица 2
| Ва-ри-ант | Силы, Н | Углы, град | M, Нм | q, H/м | а, м | ||||||

| 
| 
| 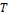
| 
| 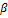
| 
| 
| ||||
| - | - | - | - | 0,6 | |||||||
| - | - | - | - | 0,6 | |||||||
| - | - | - | - | 0,5 | |||||||
| - | - | - | - | 0,5 | |||||||
| - | - | - | - | 0,8 | |||||||
| - | - | - | - | 0,8 | |||||||
| - | - | - | - | 0,6 | |||||||
| - | - | - | - | 0,6 | |||||||
| - | - | - | - | 0,6 | |||||||
| - | - | - | - | 0,8 |





Пример
 Дано: АД=ДЕ=СК=KN=NL=
Дано: АД=ДЕ=СК=KN=NL=  , СE=LH=HB=
, СE=LH=HB= 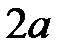 ,
,
F=2000H,
P=1000H,
T=1500H,
M=-1500Hм,
q=500H/м,
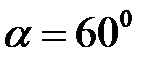 ,
,
 ,
,
 ,
,
 =0,8 м
=0,8 м
____________

1. Устанавливаем число неизвестных: в т. А – реакция 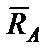 , в т. С – две составляющие
, в т. С – две составляющие  и
и  внутренней реакции
внутренней реакции  , в т. В – две силы
, в т. В – две силы  ,
,  и пара сил с моментом МВ (всего 6 неизвестных). Уравнений равновесия для данной системы тел можно составить 6 (по 3 для каждого из двух тел, входящих в систему), значит, она статически определима.
и пара сил с моментом МВ (всего 6 неизвестных). Уравнений равновесия для данной системы тел можно составить 6 (по 3 для каждого из двух тел, входящих в систему), значит, она статически определима.
2. Разбиваем систему на отдельные тела по соединительному шарниру С: балка АС и г-образная балка CLB.Прикладываем к каждой балке действующие на неё силы, включая реакции отброшенных внешних связей (это сила  для балки АС, силы
для балки АС, силы  ,
,  и пара с моментом МВ для балки CLB). Внутренняя реакция в шарнире С (равная нулю, если рассматривается система тел как одно целое) учитывается, когда систему расчленяем на две отдельные балки. По аксиоме равенства действия противодействию, две балки АС и CLB действуют друг на друга в т.С с силами равными по модулю, противоположными по направлению, т.е.
и пара с моментом МВ для балки CLB). Внутренняя реакция в шарнире С (равная нулю, если рассматривается система тел как одно целое) учитывается, когда систему расчленяем на две отдельные балки. По аксиоме равенства действия противодействию, две балки АС и CLB действуют друг на друга в т.С с силами равными по модулю, противоположными по направлению, т.е.
 = -
= -  .
.
Эти силы на рисунках показаны через составляющие по осям X и Y. Так как направления составляющих указано на рисунках (для балки АС их направление совпадает с положительным направлением осей - см. рис. 1, а
для балки CLB - противоположно - рис. 2), при расчётах принимается во внимание равенство их модулей, т.е.
 ;
; 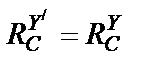 .
.
3. Рассматриваем равновесие каждого тела в отдельности.
3.1. Рассмотрим равновесие балки АС (смотри рис.16)

Балка находится в равновесии под действием плоской произвольной системы сил, являющейся уравновешенной
(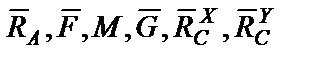 )~0,
)~0,
где 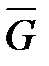 - равнодействующая распределённой силы, давящей на балку с интенсивностью q по отрезку СЕ.
- равнодействующая распределённой силы, давящей на балку с интенсивностью q по отрезку СЕ.
Сила 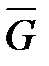 приложена перпендикулярно отрезку к его середине, а её модуль равен
приложена перпендикулярно отрезку к его середине, а её модуль равен

Прежде чем составлять уравнения равновесия, надо на рисунке показать координатные оси X и Y (направлять их надо так, чтобы они были перпендикулярны наибольшему количеству неизвестных сил). Заданные силы рекомендуется разложить на составляющие по выбранным осям (для силы  показано на рис. 16).
показано на рис. 16).
Система сил, приложенная к балке АС, является плоской произвольной. Для неё можно составить три уравнения равновесия – два уравнения проекций сил на каждую из координатных осей и одно уравнение моментов
(сумму моментов надо брать относительно той точки, через которую проходят линии действия наибольшего количества неизвестных сил, в нашем случае это т.С).
 (4)
(4)
 (5)
(5)
 (6)
(6)
3.2. Рассмотрим равновесие г-образной балки CLB (см. рис.17)
Эта балка находится в равновесии под действием плоской произвольной уравновешенной системы сил
( )~0
)~0
Показываем на рисунке все действующие на балку силы, включая реакции отброшенных связей. В т. С реакция связи выражена через составляющие
 ;
;  .
.
Проводим координатные оси (направление их должно быть таким же, как на рис. 16), раскладываем заданные силы на составляющие и составляем уравнения равновесия. Их, так же как и для первой балки, должно быть три.

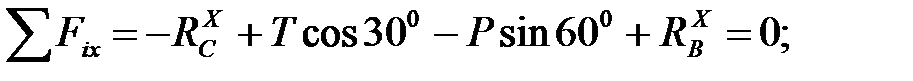 (7)
(7)
 (8)
(8)
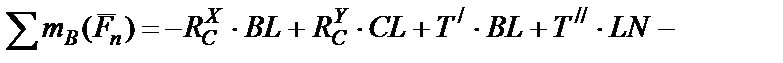

или
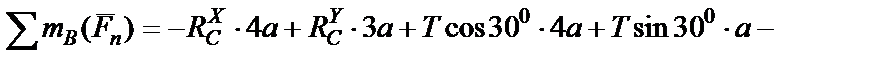
 (9)
(9)
При составлении уравнения моментов (сумма моментов сил взята относительно т. В) для определения момента силы  использована теорема Вариньона.
использована теорема Вариньона.
4. Решаем все 6 полученных уравнений совместно
Из (4):

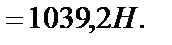
Из (6):


Из (5):


Из (7):
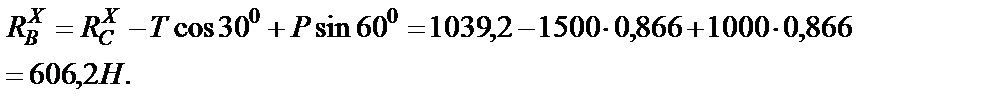
Из (8):

Из (9):

5. Проверка
Рассматриваем равновесие составной балки ACLB, считая её одним твердым телом. Система сил, действующая на неё является уравновешенной (реакция в шарнире С – в данном случае внутренняя – не учитывается, так как равна нулю).
( )~0
)~0

Составим только одно уравнение равновесия 
Подставляем все найденные неизвестные в выражение (10)

или
 В результате
В результате
10535,6-10535,6=0.
Все неизвестные найдены правильно.
Ответ: 


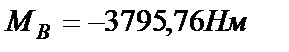
Задача 3 (С3). Тема: Равновесие пространственной системы произвольных сил.
Задание: Прямоугольная однородная плита 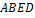 весом
весом  удерживается в положении, показанном на рисунке 19. К плите приложена сила
удерживается в положении, показанном на рисунке 19. К плите приложена сила  , величина которой, а также размеры и вес плиты указаны в таблице 3. Определить реакции опор плиты, учитывая, что она находится в равновесии.
, величина которой, а также размеры и вес плиты указаны в таблице 3. Определить реакции опор плиты, учитывая, что она находится в равновесии.
Таблица 3
| Вари-ант |  ,
H ,
H
|  H
H
|  град.
град.
| 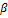 ,
град. ,
град.
|  ,
м ,
м
| 

| 

|
| 1,5 | 0,8 | 0,6 | |||||
| 2,0 | 1,2 | 1,0 | |||||
| 1,8 | 1,2 | 0,9 | |||||
| 2,2 | 1,6 | 1,0 | |||||
| 2,4 | 1,8 | 1,2 | |||||
| 1,6 | 0,8 | 0,8 | |||||
| 2,0 | 1,5 | 1,0 | |||||
| 2,2 | 1,8 | 1,2 | |||||
| 2,4 | 1,6 | 1,0 | |||||
| 2,8 | 1,6 | 1,2 |





Алгоритм решения задачи покажем на следующем примере.

Дано:
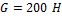 ;
; 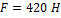 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
; 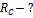
1. Рассмотрим равновесие плиты 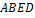 .
.
2. Покажем заданные силы, приложенные к плите:  и
и  . Силу
. Силу  разложим на составляющие (
разложим на составляющие ( по оси
по оси  по оси
по оси  ). Сила тяжести
). Сила тяжести  (вес – это модуль силы тяжести) приложена в центре тяжести плиты – т. К (находится на пересечении диагоналей прямоугольника
(вес – это модуль силы тяжести) приложена в центре тяжести плиты – т. К (находится на пересечении диагоналей прямоугольника 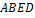 ) и направлена вертикально вниз (параллельно оси
) и направлена вертикально вниз (параллельно оси  ).
).
3. Устанавливаем связи данной плиты и заменяем их реакциями. У плиты имеются три связи (опоры): в точке А – сферический шарнир, реакцию  его показываем через три составляющие по координатным осям (
его показываем через три составляющие по координатным осям ( , в точке В – цилиндрический шарнир или пара, реакцию
, в точке В – цилиндрический шарнир или пара, реакцию  , расположенную в плоскости, перпендикулярной оси шарнира (оси
, расположенную в плоскости, перпендикулярной оси шарнира (оси  ), показываем через две составляющие
), показываем через две составляющие  , в точке С стержень, его реакция
, в точке С стержень, его реакция  направлена по стержню (см. рисунок 20), ее разложим на составляющие
направлена по стержню (см. рисунок 20), ее разложим на составляющие  по осям
по осям 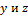 соответственно.
соответственно.
4. Из равновесия пространственной системы сил (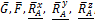
 ,
,  ) получим шесть уравнений равновесия (неизвестных сил тоже шесть – они снизу подчеркнуты одной чертой):
) получим шесть уравнений равновесия (неизвестных сил тоже шесть – они снизу подчеркнуты одной чертой):


1.  , (11)
, (11)
где 
2.  , (12)
, (12)
где 
3.  , (13)
, (13)
где  ;
;
4. 
или
 ; (14)
; (14)
5.  ; (15)
; (15)
6. 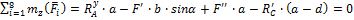 ; (16)
; (16)
5. Решаем совместно все шесть составленных уравнения
Из (11): 
Из (14):

 ;
;
Из (16):
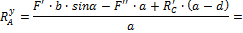
=
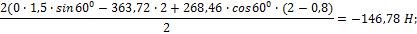
Из (15):
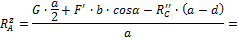

Из (12):

Из (13): 
6. Проверим полученные результаты. Для этого составим сумму моментов сил, приложенных к плите, относительно оси совпадающей со стороной ED. Эта сумма должна равняться нулю, если реакции связи найдены правильно.
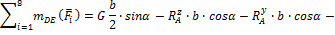



Ответ: 


КИНЕМАТИКА






