Як правило у двійкових системах будь яка помилка небажана у однаковій мірі, а втрати від правильних рішень можна вважати відсутніми, тобто r12 = r21 = rпом, r22 = r11 = 0.
Тоді
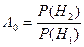
і оптимальна стратегія (59) зветься оптимальною за Котєльніковим або оптимальною за критерієм ідеального спостерігача.
При оптимальному кодуванні можна вважати P (H1) = P (H2). Тоді
Λ0 = 1.
При цій умові оптимальна стратегія (59) зветься оптимальною за критерієм максимуму відношення правдоподібності.
При роботі із пасивною паузою із критерію мінімуму середнього ризику витікає критерій Неймана-Пірсона. Його суть: найкращим є таке рішення при якому забезпечується найменша ймовірність пропуску сигналу (помилка другого роду) при фіксованій ймовірності хибного виявлення (помилка першого роду).
3.4.2. Відношення правдоподібності.
В усіх розглянутих випадках необхідно розраховувати відношення правдоподібності Λ( x ). Припустимо, що сигнали s1(t) та s2(t) повністю відомі (невідомо тільки який із них міститься у суміші x(t)), а прийом ведеться на фоні БГШ, відліки якого відповідно до (48) дорівнюють nk = xk – sk1(2). Тоді умовні щільності, які входять у відношення правдоподібності, повністю визначаються розподілом шуму.
w( x /H1(2))= 
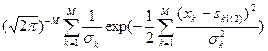, (62)
де: СКВ шуму 
.
Підставивши (62) у (60) та здійснивши скорочення, розкриття дужок і граничний перехід при M→∞ отримаємо функціонал відношення правдоподібності. Для спрощення і без порушення стратегії прийняття рішень доцільно перейти до монотонної функції від нього, а саме до логарифму
logΛ( x ) = 
. (63)
Це співвідношення необхідно порівнювати із логарифмом порогу у рамках відповідного критерію.
Враховуючи теорему Котельнікова у частині відновлення безперервного сигналу x(t) із сукупності його відліків x (з використанням ортонормованих базисних функцій) вираз (63) для випадку обробки безперервного сигналу прийме вигляд
logΛ(x) =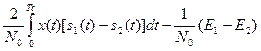 
, (64)
де: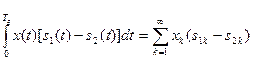 
;
енергія першого (другого) сигналу.
При застосуванні передачі з активною паузою (ФМ, ЧМ) і однаковій тривалості сигналів енергії першого та другого сигналів однакові. Тоді
logΛ(x) = 
(65)
або logΛ(x) = 
[ 
- 
] (66)
У рамках критерію максимуму відношення правдоподібності Λ0 =1, а його логарифм дорівнює 0. Це означає, що достатньо порівняти між собою кореляційні інтеграли 
та 
. Тоді стратегія прийняття рішення така:
z1 ≥z2 – справедливе рішення про наявність сигналу s1;
z1 <z2 - справедливе рішення про наявність сигналу s2.
Або: z1 –z2 ≥ 0 – прийнято s1;
(67)
z1 –z2 < 0 – прийнято s2.
(При інших критеріях z1 та z2 порівнюються у відповідних до значення logΛ0 співвідношеннях.)
3.4.3. Структура оптимальних пристроїв розрізнення двійкових сигналів.
Вираз (64) дозволяє синтезувати структурну схему пристрою оптимального демодулятора (пристрою розрізнення) сигналів, яка представлена на рис. 6.
В умовах (66,67) схема прийме вигляд, що представлено на рис. 7.
Обидві схеми передбачають перемноження прийнятої суміші з опорними сигналами та інтегрування, тобто обчислення кореляційного інтегралу. Тому таку обробку називають кореляційною. Недоліком її є необхідність знати момент приходу сигналу для синхронної подачі опорних сигналів.
Позбавленою цієї вади є фільтрова обробка, при якій величину, пропорційну кореляційному інтегралу, отримують на виході узгодженого фільтру (УФ). Цей фільтр має імпульсну характеристику
hУФ(t) = αs(Tc – t), (68)
де α – константа.
Напруга на виході такого фільтру визначається інтегралом Дюамеля
. (69)
З урахуванням (68)
. (70)
Замінивши змінну у (70) отримаємо
.
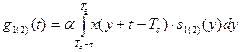Тоді на момент закінчення сигналу
.
Таким чином, отримали величину, яка з точністю до постійного множника дорівнює кореляційному інтегралу. Це підтверджує, що УФ дозволяє реалізувати алгоритм (66).
Схема фільтрового пристрою оптимального розрізнення двійкових сигналів представлена на рис.8.
При використанні у якості сигналу-носія гармонічних коливань кореляційна схема буде ефективно здійснювати розрізнення при умові співпадання моментів початку та фаз опорних сигналів з моментом приходу та фазою прийнятого сигналу. Це означає, що фаза сигналу, який приймається, повинна бути відомою. Така обробка зветься когерентною. Нажаль це далеко не завжди має місце. Фаза сигналу частіше є випадковою, тобто він є некогерентним. В таких умовах без додаткових заходів сигнал може бути втраченим (коли опорний сигнал та той, що приймається, будуть відрізнятися за фазою на 90 градусів).
Фільтрова схема може працювати і при невідомому моменті приходу сигналу, але фазочастотна характеристика узгодженого фільтру повинна бути з відємним знаком по відношенню до фазочастотного спектру сигналу.
≥ logΛ0; прий-
нято s1
x(t)
< logΛ0; прий-
нято s2
[s1(t)-s2(t)]2/N0 (E1-E2)/N0 ln(Λ0)
Рис. 6
≥0; прийня- x(t) то s1
<0; прийня-
то s2
Рис. 7.
≥0; прийнято
сигнал s1(t)
x(t)
<0; прийнято
сигнал s2(t)
Рис. 8.
3.4.4. Розрізнення некогерентних сигналів.
Некогерентний сигнал має випадкову початкову фазу. Тому у випадку, коли різниця фаз між опорним сигналом та сигналом, який приходить із каналу, буде становити π/2, корелятор видаватиме нульове значення кореляційного інтегралу. Це означає, що сигнал буде пропущено. Для подолання такого недоліку використовують квадратурну кореляційну обробку. Вона передбачає визначення модуля кореляційного інтегралу, значення якого при наявності сигналу незалежно від фази сигналу буде відмінним від нуля. Виконання такої процедури здійснюється шляхом розділення кожного із кореляторів на два підканали, різниця між якими полягає у тому, що їх опорні сигнали є ортогональними: один у вигляді синусоїди, а другий – косинусоїди. Тобто для кожного із сигналів у підканалах визначається синусний та косинусний кореляційні інтеграл 
, 
та 
, 
, які використовуються для визначення модулів кореляційного інтеграла для першого та другого сигналів Z1 = 
, Z2 =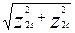 
. Отримані модульні значення кореляційних інтегралів порівнюють відповідно до зазначеної вище стратегії розрізнення двійкових сигналів.
Структура пристрою фільтрової некогерентної обробки представлена на рис. 9.
≥0; прийнято
x(t) сигнал s1(t)
<0; прийнято
сигнал s2(t)
Рис. 9.
(Більш детально про процедури некогерентного прийому дивись [1, 2, 7])
3.4.5. Показники якості розрізнення (прийому).
Якість прийому прийнято характеризувати величиною потенційної ймовірності помилки Рпом. (Вона ж є мірою потенційної завадостійкості). Мінімальна величина ймовірності помилкидосягаеться при обробці сигналів з повністю відомими параметрами і однаковими енергіями та ідеальній апаратній реалізаціїї. Відповідно до критерія максимума відношення правдоподібності величина ймовірністю помилкивизначається за формулою
Рпом = 1-Ф(
),
де: Ф(.) – інтеграл ймовірності;
Ес - енергія сигналу на вході пристрою обробки;
N0 – с пектральна щільність потужності шуму;
ρс1,с2 – нормований коефіціент взаємної кореляції першого та другого сигналів.
Величина ρс1,с2 Залежить від виду модуляції.
При однократній ФМ ρс1,с2 = -1 (сигнали є протилежними) і тоді
Рпом = 1-Ф(
).
При застосуванні ортогональних сигналів ρс1,с2 = 0 і тоді
Рпом = 1-Ф(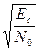
).
При АМ ρс1,с2 = ½ і тоді
Рпом = 1-Ф(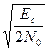
).
Залежність потенційної величини Рпом від відношення енергії сигналу (Е) до спектральної щільності шуму (No) для основних відів модуляції при когерентній бробці показана на рис.10.
Рис. 10. Залежність Рпом від відношення сигнал – шум при когерентному прийомі.
Наведені графіки показують, що найменше відношення сигнал-шум, при якому досягається однакове значення ймовірності помилки, потребує система з фазовою маніпуляцією, а найбільше – з амплітудною. Тому амплітудна маніпуляція у сучасних системах застосовується мало із–за низької завадостійкості. Найбільшу потенційну завадостійкість має фазова маніпуляція (вектори сигналів, що відповідають 0 та 1, орієнтовані у протилежні сторни). Частотна маніпуляція дещо поступається за завадостійкістю фазовій.
3.4.6. Особливості технічної реалізації розрізнення сигналів.
В залежності від виду модуляції процедура розрізнення виконується за допомогою амплітудного, частотного або фазового демодулятора відповідно.
Основою демодулятора є відповідний детектор (амплітудний, частотний, фазовий). Найбільш складною є реалізація фазової демодуляції. Тому розглянемо деякі її варіанти.
Особливістю роботи фазового детектора полягає у необхідності мати опорне коливання з частотою, що точно відповідає частоті прийнятого сигналу, і з точно визначеною відносно прийнятого сигналу фазою. Фазовий детектор здійснює порівняння фази прийнятого сигналу з фазою опорного сигналу і таким чином дає відповідь про те, який символ передавався.
Вихідний сигнал UвихФД фазового детектора пропорційний різниці фаз ∆ 
опорного сигналу і прийнятого
(або 
). ().
Формування опорного сигналу повинно здійснюватись таким чином, щоб його фаза була однаковою з фазою (“прив’язаною” до фази), однієї з посилок сигналу, що приймається (або відрізнялася від неї на відому і постійну величину). У такому випадку прийом буде зватись когерентним.
Для його реалізації опорне коливання повинно формуватися із прийнятого сигналу або фазуватися ним. Ця складна задача може вирішуватись різними способами. Одним з поширених способів при прийомі дискретних сигналів є застосування схеми Пістолькорса, суть роботи якої полягає у подвоюванні частоти прийнятого сигналу, завдяки чому ліквідуються скачки фази на π, які пов’язані з повідомленням, що передається. Після цього здійснюється ділення частоти на два. У результаті отримуємо опорне коливання на частоті сигналу але без фазової маніпуляції. При цьому сформований таким чином опорний сигнал має фазу першої прийнятої посилки сигналу.
При застосуванні відносної фазової маніпуляції можна у якості опорного сигналу використовувати коливання попередньої посилки (відносно фази якої у черговій посилці був (або не було) скачок фази на π). Для цього необхідно прийнятий сигнал подавати на сигнальний вхід ФД, а через лінію затримки (де здійснюється затримка сигналу на час тривалості посилки Тпос) подавати його на опорний вхід ФД. Такий прийом зветься автокореляційним.
Пояснення процесу демодуляції при ОВФМ.
а) автокореляційний прийом (спосіб порівняння фаз – ОФМ -1)
|
Рис. 11. Структурна схема демодулятора.
|
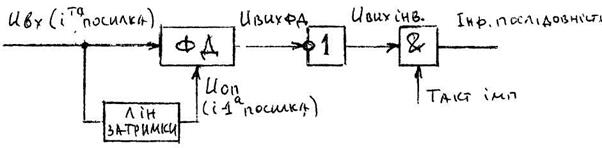
Рис. 12. Демодуляція при автокореляційному прийомі.
б) спосіб порівняння полярностей – ОФМ – 2.
|
Рис. 13.Структурна схема демодулятора.
|
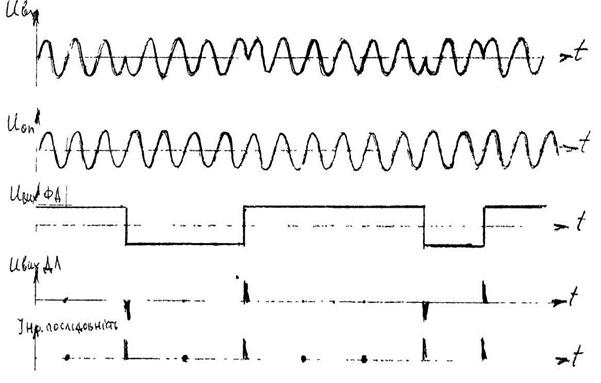
Рис. 14. Процес демодуляції при порівнянні полярностей.
Серед двох представлених методів демодуляції сигналів з ОВФМ дещо більшу завадостійкість має другий. Крім того, автокореляційний метод викликане труднощі при виготовленні прецезіонної лінії затримки.
Комплексне завдання
1. По каналу зв’язку передаються повідомлення x1, x2,... xN , імовірності яких надані у таблиці 1кз.
1.1. Визначити:
власну ентропію джерела,
максимальну ентропію джерела,
надлишковість джерела,
швидкість передачі інформації при наявності завад,
швидкість передачі інформації при відсутності завад,
пропускну здатність каналу при наявності завад,
пропускну здатність каналу при відсутності завад.
(Канал вважати симетричним)
Проаналізувати результати.
Таблиця 1кз
| Вариант | P(x1) | P(x2) | P(x3) | P(x4) | P(x5) | Тривалість посилки (Тпос) | Pпом |
| 1 (16) | P(x1) = 0,2 | P(x2) = 0,1 | P(x3) = 0,3 | P(x4) = 0,25 | P(x5) = …… | 10мкс | 0.1 |
| 2 (17) | P(x1) = 0,1 | P(x2) = 0,2 | P(x3) = 0,4 | P(x4) = 0,25 | P(x5) = …… | 20мс | 0.2 |
| 3 (18) | P(x1) = 0,4 | P(x2) = 0,1 | P(x3) = 0,3 | P(x4) = 0,15 | P(x5) = …… | 25мкс | 0.3 |
| 4 (19) | P(x1) = 0,2 | P(x2) = 0,4 | P(x3) = 0,3 | P(x4) = 0,05 | P(x5) = …… | 50мс | 0.4 |
| 5 (20) | P(x1) = 0,1 | P(x2) = 0,1 | P(x3) = 0,3 | P(x4) = 0,25 | P(x5) = ……. | 1мкс | 0.5 |
| 6 (21) | P(x1) = 0,2 | P(x2) = 0,1 | P(x3) = 0,6 | P(x4) =..... | 100мкс | 0.01 | |
| 7 (22) | P(x1) = 0,2 | P(x2) = 0,3 | P(x3) = 0,25 | P(x4) =..... | 40мкс | 0.02 | |
| 8 (23) | P(x1) = 0,4 | P(x2) = 0,15 | P(x3) = 0,3 | P(x4) =..... | 25мс | 0.25 | |
| 9 (24) | P(x1) = 0,2 | P(x2) = 0,4 | P(x3) = 0,35 | P(x4) =... | 10мс | 0.15 | |
| 10 (25) | P(x1) = 0,1 | P(x2) = 0,2 | P(x3) = 0,3 | P(x4) =.... | 125мкс | 0.2 | |
| 11 (26) | P(x1) = 0,1 | P(x2) = 0,2 | P(x3) = 0,15 | P(x4) = 0,25 | P(x5) = …… | 10мкс | 0.1 |
| 12 (27) | P(x1) = 0,2 | P(x2) = 0,1 | P(x3) = 0,4 | P(x4) = 0,25 | P(x5) = …… | 200мкс | 0.25 |
| 13 (28) | P(x1) = 0,2 | P(x2) = 0,1 | P(x3) = 0,3 | P(x4) = 0,15 | P(x5) = …… | 1мс | 0.3 |
| 14 (29) | P(x1) = 0,1 | P(x2) = 0,25 | P(x3) = 0,3 | P(x4) = 0,05 | P(x5) = …… | 25мс | 0.4 |
| 15 (30) | P(x1) = 0,1 | P(x2) = 0,2 | P(x3) = 0,15 | P(x4) = 0,25 | P(x5) = ……. | 4мс | 0.02 |
1.2. Розрахувати пропускну здатність безперервного каналу при умові, що його смуга узгоджена із сигналом,який використовується при передачі інформації у першій задачі, а відношення потужності сигналу до потужності шуму становить:
для 1; 11; 21; 31 варіантів 3Дб;
для 2; 12; 22; 32 варіантів 6Дб;
для 3; 13; 23; 33 варіантів 9Дб;
для 4; 14; 24; 34 варіантів 10Дб;
для 5; 15; 25; 35 варіантів 13Дб;
для 6; 16; 26; 36 варіантів 16Дб;
для 7; 17; 27; 37 варіантів 20Дб;
для 8; 18; 28; 38 варіантів 23Дб;
для 9; 19; 29; 39 варіантів 26Дб;
для 10; 20; 30; 40 варіантів 30Дб.
2. Визначити кількість інформації, що міститься у вашому прізвищі, імені та по батькові, вважаючи, що алфавіт складається з 32 літер, у двох випадках:
а) поява будь-якої літери на будь-якому місці рівноімовірна;
б) з урахуванням реальної нерівноімовірності використання літер.
Примітка: спиратися на дані [3].
3. Дослідити процеси кодування та декодування двійкового повідомлення завадостійким циклічним кодом.
Представити свої ініціали у двійковому коді (код обрати за власним вибором: міжнародний телеграфний код МТК2 (Додаток 1); МТК5 (Додаток 2); за номером літери у алфавіті; у коді АSCII, тощо), після чого:
а) визначити відстань Хемінга між комбінаціями першою та другою, другою та третьою, першою та третьою літер;
б) закодувати кожну із літер завадостійким циклічним кодом, який задається кодоутворюючим поліномом, взятим із табл. Додаток 2. (номер варіанта визначається номером у списку групи).
При цьому необхідно:
- отримати залишки шляхом ділення інформаційних складових на утворюючий поліном;
- сформувати кодові слова, якими повинні бути представлені літери ініціалів при передачі їх в каналі зв’язку;
- перевірити правильність сформованих кодових слів шляхом ділення їх на утворюючий поліном (залишки повинні дорівнювати нулю);
в) визначити кодову відстань між представленими у циклічному коді літерами ініціалів;
г) перевірити здатність коду виявити помилки певної кратності, для чого ввести помилки у вигляді багаточлена помилки Е(х), взятого з табл.. Додаток 2, (або за завданням викладача), додавши його до багаточленів кодових слів першої, другої та третьої літер;
д) визначити надлишковість та відносну швидкість коду;
є) визначити, чи може код забезпечити виявлення помилок кратності 2 та 3;
е) у відповідності з кодоутворюючим поліномом розробити функціональну схему кодуючого пристрою;
ж) відобразити процес отримання залишку (у вигляді двійкової послідовності) шляхом покрокового заповнення таблиці стану тригерів регістру кодуючого пристрою (для кожної літери);
з) відобразити процес отримання синдрому (залишку) при декодуванні у відсутності помилок шляхом покрокового заповнення таблиці стану тригерів регістру декодуючого пристрою (для першої та другої літери);
і) відобразити процес отримання синдрому при декодуванні спотворених кодових слів першої, другої та третьої літер шляхом покрокового заповнення таблиці стану тригерів регістру декодуючого пристрою.
к) порівняти та проаналізувати результати, отримані вище.
4. Дослідити процеси модуляції та демодуляції при застосуванні фазових методів передачі двійкових повідомлень:
а) відобразити епюри, що ілюструють процес модуляції при передачі дозволеної кодової комбінації першої літери Вашого ПІБ (див. п. 3) з використанням фазової маніпуляції (початкові значення фази та зв’язок фази сигналу з двійковим символом, що передається, обрати самостійно);
б) відобразити епюри, що ілюструють процес демодуляції сформованого вище сигналу;
в) відобразити епюри, що ілюструють процес модуляції при передачі коду першої літери з використанням однократної відносної фазової маніпуляції (початкові значення фази та зв’язок зсуву фази сигналу з двійковим символом, що передається, обрати самостійно);
г) відобразити процес демодуляції сформованого вище сигналу з відносною фазовою маніпуляцією при реалізації:
- автокореляційного прийому;
- при формуванні опорного сигналу з використанням схеми Пістолькорса;
д) перевірити вплив фазового збою у сигналі, що приймається, або у опорному сигналі на результат демодуляції:
- ввести скачок фази на π, наприклад на початку четвертого символу (у сигнал, що приймається, або у опорний сигнал);
- відобразити процес демодуляції сигналу у зазначених умовах при використанні фазової маніпуляції;
- відобразити процес демодуляції сигналу у зазначених умовах при використанні відносної фазової маніпуляції;
- порівняти результати демодуляції і переконатися у тому, що ВФМ позбавляє від зворотної роботи (інверсного прийому), локалізуючи помилку, пов’язану із випадковим збоєм фази, тою посилкою, де він відбувся.
5. Визначити необхідні значення відношення сигнал/шум для прийому двійкового сигналу з імовірністю помилки 10-3(10-4, 10-5) при застосуванні АМ, ЧМ та ФМ. Пояснити різницю отриманих значень.
Приклад рішення:
1.1 Для визначення власної ентропії необхідно скористатися формулою Н(А)= - 
, підставивши значення ймовірностей відповідно до свого варіанту.
Максимальна ентропія визначається за формулою
Hmax(А)=logNсим.
Надлишковість ждерела визначається за формулою
R= 1 - µ =1 - 
Швидкість передачі інформації I’(A;Y)=[H(A)- H(A/Y)]/ Тпос.
У каналі без завад Iбз’(A;Y)=[H(A)]/ Тпос.
У каналі із завадами
I’зз(A;Y)=[H(A +(1-Pпом)log(1-Pпом)+Рпом log 
]/ Тпос.
Пропускна здатність каналу із завадами на символ визначається за формулою
Ссим.зз=logNсим+(1-Pпом)log(1-Pпом)+Рпом log .
Пропускна здатність каналу без завад на символ визначається за формулою
Ссим.бз=logNсим.
Пропускна здатність каналу у одиницю часу визначається за формулою
Сзз(бз) = Ссим.зз(бз)/ Тпос.
1.2 Пропускну здатність безперервного каналу розраховується за формулою 27.
2. Іваненко Петро Семенович
Словосполучення містить 24 символи, (22 літери, 2 пробіли).
