Дискретне представлення повідомлень і сигналів здійснюють з метою передачі їх у дискретному (цифровому) виді, а також для реалізації цифрових методів обробки сигналів. Основними видами дискретного представлення сигналів є дискретне узагальнене, дискретне часове і дискретне різницеве.
З прикладної точки зору найбільш поширеним є дискретне часове представлення. Воно застосовується при передачі безперервних повідомлень цифровими методами та при реалізації цифрової обробки сигналів. Суть його полягає у аналого-цифровому перетворенні сигналу. Основними складовими такого перетворення є дискретизація за часом і квантування за рівнем. Таке перетворення здійснює аналогово-цифровий перетворювач (АЦП).
Для дискретизації принципове значення має величина періоду (інтервалу) дискретизації (Tд), який визначається за теоремою Котельникова В. А. (сформулював він цю теорему у 1933р). Згідно цієї теореми будь який безперервний сигнал з обмеженим (фінітним) спектром, тобто, при умові, що його частотні складові розташовані виключно у межах від 0 до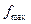 
, може бути однозначно визначений сукупністю миттєвих значень цього сигналу (відліків), взятих через інтервал часу Tд, який визначається за формулою
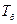
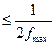, (1)
де 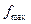- максимальна частота у спектрі сигналу.
Приклад див. на рис. 1. 1 [1].
Зворотною до періоду дискретизації величиною є частота дискретизації (Fд). Вона визначається як Fд =1/ Tд ≥ 2fmax. З урахуванням практичних рекомендацій Fд =kд 2fmax, де kд – коефіцієнтдискретизації, який більше одиниці (його рекомендовані значення становлять 1,25…2,25).
Відомо,що реальні сигнали мають кінцеву тривалість, а це означає, що їх спектр необмежений. Тому практичне застосування теореми Котельникова потребує для кожного конкретного випадку визначення величини fmax як частоти, за межами якої наявними складовими спектра можна нехтувати. Чим більшою за потужністю є частка знехтуваних складових спектру по відношенню до середньої потужності всіх складових спектру сигналу тим гіршою буде точність представлення і відновлення сигналу. Технічно обмеження спектру реалізують за допомогою фільтра нижніх частот.
Ще одною особливістю процесу дискретизації є розмноження спектру сигналу, який дискретизують. Проявляється це у появі складових спектру сигналу обапіл частот, кратних частоті дискретизації, і є наслідком модуляції дискретної послідовності коротких імпульсів, що подаються на пристрій дискретизації з періодом Tд , сигналом, який підлягає дискретизації.
У результаті дискретизації у кожний із моментів часу i 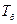отримують відлік ui, де i – номер відліку; i = 0 … Nc-1, а Nc – кількість відліків на тривалості сигналу.
Кожний з отриманих відліків ui квантують за амплітудою з кроком Δuкв. (Іноді його називають інтервалом або рівнем квантування.) При односторонньому сигналі та односторонніх шумах, на фоні яких здійснюють перетворення корисного сигналу, величина Δuкв обирається близькою (або дещо більшою) до середньоквадратичного значення амплітуди шумів (σш.ф), а при двосторонньому синалі та двосторонніх шумах величина Δuкв ≥ 2σш.ф. Такий підхід дозволяє майже виключити проходження шумового фону на вихід АЦП.
За результатом квантування значення відповідного чергового відліку сигналу приймається рівним найближчому цілому числу кроків квантування ui ≈ кΔuкв, до якого округлюється амплітуда, де к – ціле число. Тобто, при відомому значенні Δuкв кожному черговому відліку сигналу ставиться у відповідність певне ціле число. У свою чергу цю дискретну послідовність чисел представляють у вигляді послідовності кодових комбінацій (частіше всього двійкових). Таким чином, сигнал представляється послідовністю двійкових чисел. Перетворивши їх у відповідні комбінації двійкових сигналів (імпульсів тривалості τі з амплітудою U1 при наявності у певному розряді 1 та з амплітудою U0 при наявності 0) отримують сигнал, який називають цифровим.
Максимальна кількість рівнів квантування (Nр кв) визначається відношенням різниці між максимально можливим (Uс max) і мінімально можливим (Uс min) рівнями сигналу, що перетворюється, до кроку квантування Δuкв. Максимальна кількість рівнів квантування дорівнює найближчому більшому до цього відношення цілому числу
Nр кв =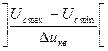 
.
Величина Nр кв обумовлює розрядність (nацп) аналогово-цифрового перетворювача, який виконує перетворення аналогового сигналу у цифровий. При двійковому кодуванні
nацп ≥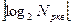 
.
Таким чином, на виході АЦП кожний відлік сигналу перетворюється у комбінацію двійкових імпульсних сигналів, яка відповідає двійковому коду значення амплітуди сигналу, вираженої з точністю до Δuкв. Таке перетворення часто називають кодово-імпульсною модуляцією (КІМ) (або імпульсно-кодовою модуляцією (ІКМ)).
Амплітудна характеристика пристрою квантування є нелінійною (ступінчатою). Її вигляд при двосторонньому синалі та двосторонніх шумах представлено на рис. 2.
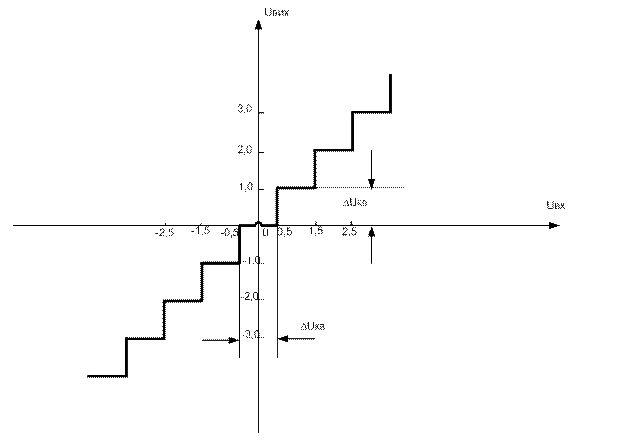Рис. 2. Амплітудна характеристика пристрою квантування.
При такій формі амплітудної характеристики сигнал на виході формується таким чином:
………
-2,5Δuкв < uвх ≤ -1, 5 Δuкв - то uвих = - 2 Δuкв;
-1,5Δuкв < uвх ≤ -0,5 Δuкв/2 - то uвих = -1 Δuкв;
-0,5 Δuкв < uвх ≤ 0,5 Δuкв - то uвих = 0;
0,5Δuк2 < uвх ≤ 1,53 Δuкв - то uвих = 1 Δuкв;
1,5Δuкв < uвх ≤ 2, 5 Δuкв - то uвих =2 Δuкв;
……..
……..
і так даді.
На превеликий жаль процедура квантування у наслідок округлення значень сигналу призводить до появи додаткових спотворень, які прийнято називати шумами квантування. Їх рівень оцінюють статистичною величиною – середньоквадратичною амплітудою шуму квантування σш.кв= Δuкв/2√3.
3.1.2.3. Векторне представлення сигналів вивчити за [1, п. 2.2; або 6 чи 7 ]
