На площині можуть бути задані тільки двомірні, або плоскі перетворення.
Рівняння 
, що зв'язує дві змінні x і y називається рівнянням лінії L в обраній плоскій системі координат, якщо координати будь-якої точки цієї лінії L задовольняють рівнянню, а будь-які інші координати точок, що не належать лінії L, не задовольняють вказаному рівнянню.
За означенням, лінія — це є співвідношення, що зв'язує координати точок деякої області простору, і, причому тільки ці координати. Рівняння являє собою аналітичний запис рівняння будь-якої плоскої лінії.
.
Якщо замість 
підставити його чисельне значення, тоді отримаємо відоме рівняння прямої
.
Отже, рівняння прямої має вигляд:
.
За умовою задачі k заданий. Точка M (x 0 , y 0) повинна також належати шуканій прямій і, за означенням лінії, перетворювати рівняння прямої в тотожність. Скористаємося цим і підставимо значення x 0 і y 0 у рівняння, отримаємо:
.
В останньому рівнянні невідоме b. Елементарним перетворенням з останнього рівняння отримаємо
.
Знайдене b підставимо в рівняння й остаточно отримаємо:
.
Останнє рівняння є рівнянням прямої, що проходить через дану точку в заданому напрямку.
Невідомий k - кутовий коефіцієнт нахилу лінії стосовно додатного напрямку осі 0 X. Однак, знаючи загальний вид рівняння прямої (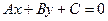
) і з огляду на те, що обидві точки розташовані на шуканій лінії, можна скласти наступну систему:
,
де 
– координати точок M 1 і M 2 відповідно, (відомі), а k і b – шукані невідомі. Віднімаючи від першого рівняння друге, виразимо k,
.
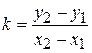Підставимо знайдене k у кожне з рівнянь і визначимо b
.
Підставимо знайдені k і b у рівняння прямої
.
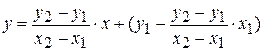Перетворимо останнє рівняння
і остаточно
.
Дане рівняння називається рівнянням прямої, що проходить через дві точки.
Означення. Рівнянням лінії називається співвідношення y = f(x) між координатами точок, які складають цю лінію.
Означення. Будь-яка пряма на площині може бути задана рівнянням першого порядку
Ах + Ву + С = 0,
причому сталі А, В не рівні нулеві одночасно, тобто А2 + В2 ¹ 0. Це рівняння першого порядку називають загальним рівнянням прямої.
В залежності від значень сталих А,В і С можливі наступні частинні випадки:
- C = 0, А ¹ 0, В ¹ 0 – пряма проходить через початок координат,
- А = 0, В ¹ 0, С ¹ 0 { By + C = 0} - пряма паралельна осі Ох,
- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – пряма паралельна осі Оу,
- В = С = 0, А ¹ 0 – пряма співпадає з віссю Оу,
- А = С = 0, В ¹ 0 – пряма співпадає з віссю Ох.
Означення. У декартовій прямокутній системі координат вектор з компонентами (А, В) перпендикулярний до прямої, заданої рівнянням Ах + Ву + С = 0.
Нехай у просторі задано дві точки M1(x1, y1, z1) і M2(x2, y2, z2), тоді рівняння прямої, яка проходить через ці точки:
.
Якщо який-небудь із знаменників дорівнює нулеві, необхідно прирівняти нулеві відповідний чисельник.
Якщо загальне рівняння прямої Ах + Ву + С = 0 привести до вигляду:
і позначити 
, то отримане рівняння називається рівнянням прямої з кутовим коефіцієнтом k.
Означення. Кожен ненульовий вектор 
=(a1, a2), компоненти якого задовольняють умову Аa1 + Вa2 = 0 називається напрямним вектором прямої
Ах + Ву + С = 0.
Якщо у загальному рівнянні прямої Ах + Ву + С = 0, С ¹ 0, то, розділивши на – С, отримаємо: 
або
,
де 
Геометричний зміст коефіцієнтів у тому, що коефіцієнт а є координатою точки перетину прямої з віссю Ох, а b – координатою точки перетину прямої з віссю Оу.
Якщо обидві частини рівняння Ах + Ву + С = 0 розділити на число 
, яке називається нормуючим множником, то отримаємо
xcosj + ysinj - p = 0 – нормальне рівняння прямої.
Знак ± нормуючого множника необхідно вибирати так, щоб m×С < 0.
р – довжина перпендикуляра, опущеного з початку координат на пряму, а j - кут, утворений цим перпендикуляром з додатнім напрямом осі Ох.
Означення. Якщо задані дві прямі y = k1x + b1, y = k2x + b2, то гострий кут між цими прямими буде визначатися як
.
Дві прямі паралельні, якщо k1 = k2.
Дві прямі перпендикулярні, якщо k1 = -1/k2.
Теорема. Прямі Ах + Ву + С = 0 і А1х + В1у + С1 = 0 паралельні, коли пропорціональні коефіцієнти А1 = lА, В1 = lВ. Якщо і С1 = lС, то прямі співпадають.
Координати точки перетину двох прямих знаходяться як розв’язок системи двох рівнянь.
Означення. Пряма, яка проходить через точку М1(х1, у1) і перпендикулярна до прямої у = kx + b представляється рівнянням:
.
Теорема. Якщо задана точка М(х0, у0), то відстань до прямої Ах + Ву + С =0 визначається так
.
Площина та пряма в просторі
Будь-яка поверхня є геометричним місцем точок, її складових, які визначаються рівнянням
.
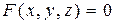Іншими словами, усі точки, що задовольняють цьому рівнянню, будуть належати поверхні.
Нехай у просторі XYZ задана площина a і до неї в точці K проведемо вектор нормалі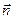 
. Оскільки площина a орієнтована довільно в просторі, то вектор 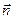буде утворювати з осями x, y, z кути a, b і g відповідно.
Виберемо на площині a точку M, що не збігається з K і сполучимо з цією точкою вектор 
. Очевидно, що 
, де r – модуль вектора 
, з рівняння отримаємо нормальне рівняння площини: 
.
Однак, якщо представимо вектор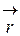 
як 
, а вектор 
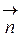
, тоді підставивши отримані вирази, отримаємо 
.
Знаючи, що для будь-якої точки, що належить площині, з координатами (A,B.C) можна обчислити напрямні косинуси
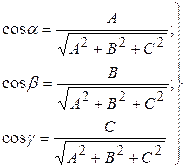
з врахуванням яких загальне рівняння прямої можна перетворити на
,
яке відомо, як рівняння площини.
Прямою лінією назвемо перетин двох площин у просторі. Визначення можна записати математично як 
.
Нехай площини a і b задані рівняннями:
і
,
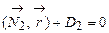де 
; 
, 
,
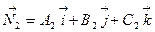система з цих рівнянь:
Вказані рівняння називаються загальними рівняннями прямої в просторі, записаними у векторній формі.
Означення. Площиною називається поверхня, всі точки якої задовольняють загальне рівняння:
Ax + By + Cz + D = 0,
де А, В, С – координати вектора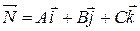 
- вектор нормалі до площини.
Можливі наступні частинні випадки:
А = 0 – площина паралельна осі Ох,
В = 0 – площина паралельна осі Оу,
С = 0 – площина паралельна осі Оz,
D = 0 – площина проходить через початок координат,
А = В = 0 – площина паралельна площині хОу,
А = С = 0 – площина паралельна площині хОz,
В = С = 0 – площина паралельна площині yOz,
А = D = 0 – площина проходить через вісь Ох,
В = D = 0 – площина проходить через вісь Оу,
С = D = 0 – площина проходить через вісь Oz,
А = В = D = 0 – площина співпадає з площиною хОу,
А = С = D = 0 – площина співпадає з площиною xOz,
В = С = D = 0 – площина співпадає з площиною yOz.
