Тема 2. Елементи векторної алгебри та аналітичної геометрії
Лекція 2.1. Вектори на площині і у просторі. n-вимірний вектор і векторний простір. Скалярний векторний та мішаний добуток векторів, їх застосування. Пряма на площині. Основні рівняння. Площина та пряма в просторі
Вектори на площині і у просторі. n-вимірний вектор і векторний простір
Лінійні операції (додавання, віднімання, множення на число) визначені для кожної множини (числа, многочленів, векторів, матриць). Самі операції різні, але їх властивості однакові.
Для того, щоб дати означення лінійного (векторного) простору розглянемо деяку множину L дійсних чисел (п -вимірний вектор), для яких визначені операції додавання і множення на число.
Означення. п -вимірним вектором називається упорядкована сукупність п дійсних чисел, які записуються у вигляді  , де
, де  - і-та компонента вектора
- і-та компонента вектора  .
.
Два п -вимірних вектори рівні тоді і тільки тоді, коли рівні їх відповідні компоненти, тобто  , якщо
, якщо 
 .
.
Сумою двох векторів однакової розмірності п називається вектор  , компоненти якого дорівнюють сумі відповідних компонент векторів, які додаються, тобто
, компоненти якого дорівнюють сумі відповідних компонент векторів, які додаються, тобто  ,
,  .
.
Добутком вектора  на дійсне число
на дійсне число  називається вектор
називається вектор  , компоненти
, компоненти  якого дорівнюють добутку
якого дорівнюють добутку  на відповідні компоненти вектора
на відповідні компоненти вектора  , тобто
, тобто  ,
,  .
.
Лінійні операції над будь-якими векторами мають такі властивості:
1) Комутативність  +
+  =
=  +
+  .
.
2) Асоціативність ( +
+  ) +
) +  =
=  + (
+ ( +
+  ).
).
3) Існує такий нульовий вектор 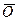 , що
, що 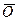 +
+  =
=  для "
для "  Î L.
Î L.
4) Для "  Î L існує вектор
Î L існує вектор  = -
= -  , такий, що
, такий, що  +
+  =
= 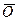 .
.
5) 1×  =
=  .
.
6) a(b  ) = (ab)
) = (ab)  .
.
7) Розподільний закон (a + b)  = a
= a  + b
+ b  .
.
8) a( +
+  ) = a
) = a  + a
+ a  .
.
Означення. Множина L називається лінійним (векторним) простором, а його елементи називаються векторами.
Властивості лінійних просторів.
1) У кожному лінійному просторі існує тільки один нульовий елемент.
2) Для кожного елемента існує тільки один протилежний елемент.
3) Для кожного  Î L справедлива рівність 0×
Î L справедлива рівність 0×  = 0.
= 0.
4) Для кожного a Î R і 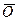 Î L справедлива рівність a×
Î L справедлива рівність a× 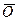 =
= 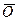 .
.
5) Якщо a×  =
= 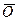 , то a = 0 або
, то a = 0 або  =
= 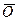 .
.
6) (-1)  = -
= -  .
.
Вектори та дії над ними
Величини називають скалярними (скалярами), якщо вони після вибору одиниць вимірювання повністю характеризуються одним числом.
Якщо деяка скалярна величина повністю визначається одним числом, що не залежить від вибору осей відліку, то тоді говорять про чисту скалярну величину або про істинний скаляр.
Якщо деяка скалярна величина визначається одним числом, абсолютна величина якого не залежить від вибору осей відліку, а її знак залежить від вибору позитивного напрямку на осях координат, то тоді говорять про псевдоскалярну величину.
Величина називається вектором (векторною), якщо вона визначається двома елементами різної природи: алгебраїчним елементом - числом, що показує довжину вектора і скаляром, що є, і геометричним елементом, що вказує напрямок вектора.
Геометрично прийнято зображати вектор напрямленим відрізком. Знаючи координати початку і кінця вектора  і
і  , можна знайти координати вектора, зумовленого цими точками
, можна знайти координати вектора, зумовленого цими точками  , тобто від координат кінця віднімають координати початку вектора.
, тобто від координат кінця віднімають координати початку вектора.

Рис. 1.
Додавання і віднімання
Додавання і віднімання векторів здійснюють геометрично (рис.1.). Цей спосіб називають правилом трикутника.
Математично додавання записують  або
або  , якщо мова йде про віднімання векторів (рис. 1).
, якщо мова йде про віднімання векторів (рис. 1).
Якщо в просторі задано кілька векторів, число яких більше двох, то операцію додавання (віднімання) записують як  Геометрично цей спосіб називають правилом багатокутника.
Геометрично цей спосіб називають правилом багатокутника.
Множення вектора на скалярну величину. При множенні вектора  на скаляр a отримують новий вектор
на скаляр a отримують новий вектор  , що збігається по своєму типі з вихідним, довжина (модуль) якого змінюється в a разів, а напрямок збігається з напрямком вихідного вектора
, що збігається по своєму типі з вихідним, довжина (модуль) якого змінюється в a разів, а напрямок збігається з напрямком вихідного вектора  , якщо a > 0, або протилежний вихідному векторові, якщо a < 0. У координатній формі, якщо
, якщо a > 0, або протилежний вихідному векторові, якщо a < 0. У координатній формі, якщо  , те
, те 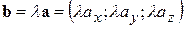 .
.

Рис.2.
Два однаково напрямлених і паралельних вектори називають колінеарними. Колінеарні вектори можуть бути різної довжини
Два вектори  і
і 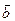 називають колінеарними, якщо існують такі два числа a і b, не рівні нулеві одночасно, що виконується рівність
називають колінеарними, якщо існують такі два числа a і b, не рівні нулеві одночасно, що виконується рівність 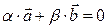 .
.
Три вектори  ,
, 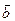 і
і  назвемо компланарними, якщо існують такі три числа a, b і g, не рівні одночасно нулеві, що виконується рівність
назвемо компланарними, якщо існують такі три числа a, b і g, не рівні одночасно нулеві, що виконується рівність  .
.
Довжина вектора в координатах визначається як відстань між точками початку та кінця вектора. Якщо задано дві точки у просторі А(х1, y1, z1), B(x2, y2, z2), то  .
.
Якщо М(х, у, z) ділить відрізокАВ у відношенні l/m, то координати цієї точки определяются как:
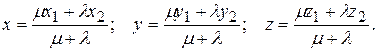
Частинним випадком є відшукання координат середини відрізка:

Лінійна залежність та незалежність системи векторів
Розглянемо систему з т п -вимірних векторів

За означенням дані вектори називаються лінійно залежними, якщо рівність

Можлива за умови, що хоча б одне з чисел 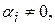 де
де  Якщо ж наведена рівність можлива лише за умови,
Якщо ж наведена рівність можлива лише за умови,  то вектори називаються лінійно незалежними.
то вектори називаються лінійно незалежними.
Властивості поняття лінійної залежності:
1. якщо серед векторів є нульовий, то ці вектори лінійно залежні;
2. якщо вектори лінійно залежні, то після додавання до них одного чи кількох нових векторів дістанемо лінійно залежну систему векторів;
3. якщо вектори лінійно незалежні, то після відкидання одного чи кількох векторів дістанемо знову лінійно незалежні вектори;
4. вектори лінійно залежні тоді і тільки тоді, коли один з них є лінійною комбінацією інших;
5. якщо два ненульові тривимірні вектори лінійно залежні, то вони колінеарні, і навпаки;
6. якщо три ненульові тривимірні вектори лінійно залежні, то вони компланарні, і навпаки;
7. чотири (і більше) тривимірних вектори зажди лінійно залежні.






