ЛІНІЙНОГО ПРОГРАМУВАННЯ
Мета роботи – вміння розв’язувати задачі оптимізації з використання лінійного програмування в OpenOffice.org Calc.
Завдання для підготовки до виконання лабораторної роботи
1 Визначити оптимальні параметри суміші для складання дієти, враховуючи змінні як невід’ємні значення (табл.5.1). Параметри, які необхідні для розв’язання задачі наступні: p, r, u, w, ai, bi, ci, di, fi (i=1,5)
Фірма займається складанням дієти, в якій присутні p одиниць білків, r одиниць вуглеводів, u одиниць жирів і w одиниць вітамінів. Як дешевше досягти цього при наведених в табл. 5.2 цінах (в гривнях) на 1 кг (або 1 л) п’яти продуктів, що має фірма?
2 Визначити скільки і яких пакетів добрив необхідно купити, щоб забезпечити ефективність ґрунту у газоні и мінімізувати ціну пакета з добривами (табл.3.3). Параметри, які необхідні для розв’язання задачінаступні a1, a2, a3, b1, b2, b3, c1, c2, c3, s1, s2.
Фірма випускає два пакети добрив для газонів: стандартний і поліпшений. В стандартний пакет входять a1 кг азотних, a2 кг фосфорних та a3 кг калійних добрив, а в поліпшений – b1 кг азотних, b2 кг фосфорних та b3 кг калійних добрив. Відомо, що для конкретного газону потребується щонайменше c1 кг азотних, c2 кг фосфорних та c3 кг калійних добрив. Стандартний пакет коштує s1 грн, а поліпшений – s2 грн.
Таблиця 5.1 – Змінні для задачі про складання дієти
| Продукти | Хліб | соя | Сушена риба | фрукти | молоко |
| Білки | a1 | a2 | a3 | a4 | a5 |
| Вуглеводи | b1 | b2 | b3 | b4 | b5 |
| Жири | c1 | c2 | c3 | c4 | c5 |
| Вітаміни | d1 | d2 | d3 | d4 | d5 |
| Ціна | f1 | f2 | f3 | f4 | f5 |
Таблиця 5.2 – Варіанти до визначення оптимальних параметрів суміші для складання дієти
| Номер варіанта | Вхідні дані | ||||
| p=25, r=32, u=23, w=25 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=15 | f2=33 | f3=31 | f4=25 | f5=22 | |
| p=15, r=30, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=34 | f4=21 | f5=22 | |
| p=15, r=30, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=7 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=23 | f5=21 | |
| p=18, r=30, u=20, w=32 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=3 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=12 | f2=30 | f3=31 | f4=25 | f5=22 | |
| p=15, r=30, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=34 | f4=25 | f5=26 | |
| p=25, r=20, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=15 | f2=29 | f3=30 | f4=23 | f5=26 | |
| p=15, r=30, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=16 | f2=28 | f3=34 | f4=25 | f5=28 | |
| p=15, r=30, u=15, w=40 | a1=2 | a2=3 | a3=8 | a4=4 | a5=2 |
| b1=10 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=1 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=18 | f5=22 |
Продовження табл. 5.2
| p=22, r=30, u=20, w=28 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=4 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=34 | f3=31 | f4=25 | f5=22 | |
| p=15, r=30, u=15, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=6 |
| b1=10 | b2=4 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=4 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=25, r=30, u=15, w=30 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=19, r=30, u=21, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=8 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=22, r=30, u=25, w=23 | a1=7 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=1 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=1 | d2=2 | d3=6 | d4=6 | d5=2 | |
| f1=19 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=20, r=35, u=15, w=30 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=1 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=25, r=10, u=15, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=2 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=12 | c3=3 | c4=1 | c5=4 | |
| d1=1 | d2=2 | d3=0 | d4=7 | d5=2 | |
| f1=15 | f2=30 | f3=30 | f4=25 | f5=10 | |
| p=12, r=30, u=18, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=12 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=10 | c3=3 | c4=1 | c5=4 | |
| d1=2 | d2=2 | d3=0 | d4=9 | d5=2 | |
| f1=15 | f2=30 | f3=30 | f4=25 | f5=10 | |
| a1=2 | a2=3 | a3=7 | a4=4 | a5=2 | |
| b1=12 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=10 | c3=3 | c4=1 | c5=4 | |
| d1=2 | d2=2 | d3=0 | d4=9 | d5=2 | |
| f1=15 | f2=30 | f3=30 | f4=25 | f5=10 |
Продовження табл. 5.2
| p=15, r=30, u=15, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=12 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=10 | c3=3 | c4=1 | c5=4 | |
| d1=2 | d2=2 | d3=0 | d4=9 | d5=2 | |
| f1=15 | f2=30 | f3=30 | f4=25 | f5=10 | |
| p=20, r=32, u=18, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=12 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=10 | c3=3 | c4=1 | c5=4 | |
| d1=2 | d2=2 | d3=0 | d4=9 | d5=2 | |
| f1=15 | f2=32 | f3=28 | f4=25 | f5=10 | |
| p=20, r=15, u=25, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=12 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=0 | c2=10 | c3=3 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=0 | d4=9 | d5=2 | |
| f1=15 | f2=30 | f3=28 | f4=25 | f5=10 | |
| p=18, r=30, u=17, w=40 | a1=3 | a2=5 | a3=7 | a4=4 | a5=1 |
| b1=10 | b2=4 | b3=1 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=1 | |
| d1=4 | d2=2 | d3=5 | d4=6 | d5=7 | |
| f1=17 | f2=30 | f3=30 | f4=14 | f5=20 | |
| p=25, r=30, u=15, w=30 | a1=3 | a2=5 | a3=7 | a4=4 | a5=1 |
| b1=10 | b2=4 | b3=1 | b4=2 | b5=3 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=1 | |
| d1=4 | d2=2 | d3=5 | d4=6 | d5=7 | |
| f1=11 | f2=33 | f3=32 | f4=14 | f5=20 | |
| p=25, r=30, u=23, w=25 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=15 | f2=33 | f3=31 | f4=25 | f5=22 | |
| p=15, r=30, u=15, w=40 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=18 | f2=35 | f3=30 | f4=25 | f5=26 | |
| p=15, r=30, u=15, w=40 | a1=2 | a2=3 | a3=7 | a4=4 | a5=6 |
| b1=8 | b2=4 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=6 | c3=4 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=17 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=25, r=10, u=15, w=30 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=2 | b2=2 | b3=2 | b4=2 | b5=5 | |
| c1=0 | c2=12 | c3=3 | c4=1 | c5=4 | |
| d1=1 | d2=2 | d3=0 | d4=7 | d5=2 | |
| f1=15 | f2=30 | f3=25 | f4=25 | f5=20 |
Продовження табл. 5.2
| p=19, r=30, u=21, w=35 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=8 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=2 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=20 | f2=30 | f3=34 | f4=25 | f5=22 | |
| p=22, r=35, u=25, w=30 | a1=7 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=1 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=5 | c3=0 | c4=4 | c5=4 | |
| d1=1 | d2=2 | d3=6 | d4=6 | d5=2 | |
| f1=19 | f2=39 | f3=31 | f4=25 | f5=22 | |
| p=20, r=33, u=18, w=28 | a1=2 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=10 | b2=0 | b3=1 | b4=2 | b5=5 | |
| c1=6 | c2=8 | c3=0 | c4=7 | c5=4 | |
| d1=1 | d2=2 | d3=5 | d4=6 | d5=2 | |
| f1=20 | f2=30 | f3=35 | f4=25 | f5=22 | |
| p=25, r=30, u=15, w=30 | a1=3 | a2=5 | a3=7 | a4=4 | a5=1 |
| b1=10 | b2=4 | b3=1 | b4=2 | b5=3 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=1 | |
| d1=4 | d2=2 | d3=5 | d4=6 | d5=7 | |
| f1=11 | f2=33 | f3=32 | f4=14 | f5=20 | |
| p=25, r=30, u=23, w=25 | a1=5 | a2=3 | a3=7 | a4=4 | a5=2 |
| b1=6 | b2=4 | b3=0 | b4=2 | b5=5 | |
| c1=1 | c2=8 | c3=2 | c4=0 | c5=4 | |
| d1=2 | d2=2 | d3=4 | d4=6 | d5=2 | |
| f1=15 | f2=33 | f3=31 | f4=25 | f5=22 |
Таблиця 5.3 – Варіанти задачі про добрива для газонів
| Номер варіанта | Значення змінних | ||||||||||
| a1 | а2 | a3 | b1 | b2 | b3 | c1 | c2 | c3 | s1 | s2 | |
Продовження табл. 5.3
Загальні положення
Задачі лінійного програмування дають можливість створювати моделі оптимізаційні моделі для процесів, для яких необхідно знайти оптимальні співвідношення параметрів системи при обмеженнях, які накладено на можливі стани системи.
Постановка будь-якої задачі оптимізації починається з визначення набору незалежних змінних і звичайно включає умови, що характеризують їхні прийнятні значення. Ці умови називають обмеженнями задачі. Ще одною обов'язковою компонентою опису є скалярна міра «якості», яка має назву цільової функції, що являє собою деяку функціональну залежність від змінних. Розв’язок оптимізаційної задачі – це прийнятний набір значень змінних, якому відповідає оптимальне значення цільової функції. Під оптимальністю звичайно розуміють максимальність або мінімальність; наприклад, мова може йти про максимізацію прибутку або мінімізацію викидів шкідливих речовин.
Загальну задачу математичного програмування можна записати в наступному вигляді:
 (5.1)
(5.1)
При цьому умови виду  називаються обмеженнями-нерівностями, умови виду
називаються обмеженнями-нерівностями, умови виду  - обмеженнями-рівностями, обидва ці типи умов - функціональними обмеженнями; умова
- обмеженнями-рівностями, обидва ці типи умов - функціональними обмеженнями; умова  називається прямим обмеженням.
називається прямим обмеженням.
Опукле програмування. Задача (5.1) називається задачею опуклого програмування, якщо множина Р єопуклою, функції f, g1,..., gk опуклі на Р, функції gk+1,..., gm єлінійними. Легко перевірити, що припустима множина задачі опуклого програмування є опуклою і, отже, задача є опуклою. На розглянуту задачу поширюються твердження про властивості опуклих функцій. Теорія і чисельні методи рішення задач опуклого програмування істотно розвинені в порівнянні з загальним випадком.
Лінійне і квадратичне програмування. Задачею лінійного програмування називається задача мінімізації або максимізації лінійної функції при лінійних обмеженнях. Так, задача (5.1) є задачею лінійного програмування.
Дискретна оптимізація. Надалі будемо називати скінченні множини і рахункові множини без граничних точок дискретними. Задача (5.1) називається задачею дискретної оптимізації, якщо або сама припустима множина Х Ì Rn є дискретною, або лише деякі з координат вектора х = (x1,..., xп) мають дискретні значення на числовій осі.
Таку задачу називають задачею цілочислове програмування, якщо х Î {1,..., n }.
Очевидно, за своєю постановкою задача дискретного програмування відрізняється від загальної задачі математичного програмування спеціальним завданням прямого обмеження. Тут також використовується запис типу:
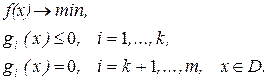 (5.2)
(5.2)
Якщо функції f, g1,..., gm є лінійними, то задачу (3.2) при J ={1,..., п } називають цілочисловою задачею лінійного програмування, а при
J¹{1,..., п} - частково цілочисловою задачею лінійного програмування.
Якщо Dj ={0, 1}, то іноді говорять про (частково) бульову задачу лінійного програмування. Ці задачі, як і звичайні задачі лінійного програмування, можуть бути подані в різних формах.
Задачі оптимізації можна розв’язувати за допомогою OpenOffice.org Calc, використовуючи СЕРВИС/ПОИСК РЕШЕНИЯ(рис. 5.1).
Для того щоб розв’язати задачу лінійного програмування в OpenOffice.org Calc, необхідно виконати наступні дії:
1. ввести умову задачі;
2. на робочому листі електронної таблиці ввести вхідні дані для змінних, формулу для цільової функції, формули для обчислення обмежень, формули для граничних умов;
3. задати у вікні ПОИСК РЕШЕНИЯ цільову функцію, граничні умови для припустимих значень змінних, співвідношення між правими і лівими частинами обмежень;
4. для розв’язання задачі встановити у вікні ПАРАМЕТРЫ РЕШЕНИЯ параметри задачі;
5. запустити задачу на виконання.

Рисунок 5.1 – Діалогове вікно ПОИСК РЕШЕНИЯ
Приклад 1 ( модельоптимізації структури виробництва, модель задачі про домішки, суміші, дієту, тощо).
Задача про суміші (задача про дієту).Фірма займається складанням дієти, в якій присутні 20 одиниць білків, 30 одиниць вуглеводів, 10 одиниць жирів і 40 одиниць вітамінів (табл.5.4). Як дешевше досягти цього при наведених в таблиці 5.4 цінах (в гривнях) за 1 кг (або 1 л) п’яти продуктів, що має фірма? Показники вмісту поживних речовин наведено у табл. 5.5.
Таблиця 5.4 – Показник цін для складових суміші
| Складові суміші | Хліб | Соя | Сушена риба | Фрукти | Молоко |
| Ціна (грн.) за одиницю товару |
Таблиця 5.5 – Показники вмісту поживних речовин для кожного зі складових суміші
| Складові суміші | Хліб | Соя | Сушена риба | Фрукти | Молоко |
| Білки | |||||
| Вуглеводи | |||||
| Жири | |||||
| Вітаміни | |||||
| Ціна |
Математична модель задачі про суміші (задача про дієту).
Змінні. Зміннимив даному випадку є:
х 1 – кількість кілограмів хліба;
х 2 – кількість кілограмів сої;
x 3 – кількість кілограмів сушеної риби.
x 4 – кількість кілограмів фруктів.
x 5 – кількість літрів молока.
Цільова функція. Вартість дієти представляється цільовою функцією Z у вигляді суми добутків кількості продуктів на їх вартісні показники, що наведені у таблиці 3.1:
Z = 12 х1 + 36 х2 + 32 х3 + 18 х4 + 10 х5.
Необхідно мінімізувати вартість, тобто мінімізувати значення цільової функції Z (Z→min).
Обмеження, які накладаються на систему (табл.5.5).
Дієта повинна мати:
20 одиниць білків
2 х 1 + 12 х 2 + 10 х 3 + 1× х 4 + 2 х 5 ³ 20.
30 одиниць вуглеводів
12 х 1 + 0× х 2 + 0× х 3 + 4 х 4 + 3 х 5 ³ 30.
10 одиниць жирів
1× х 1 + 8 х 2 + 3 х 3 + 0× х 4 + 4 х 5 ³ 10
40 одиниць вітамінів
2 х 1 + 2 х 2 + 4 х 3 + 6 х 4 + 2 х 5 ³ 40
Додаткове обмеження: невід’ємність змінних х 1, … , х 5.
Знайти
Z = 12 х 1 + 36 х 2 + 32 х 3 + 18 х 4 + 10 х 5 ® mіn
при обмеженнях
2 х 1 + 12 х 2 + 10 х 3 + 1 х 4 + 2 х 5 ³ 20,
12 х 1 + 0 х 2 + 0 х 3 + 4 х 4 + 3 х 5 ³ 30,
1 х 1 + 8 х 2 + 3 х 3 + 0 х 4 + 4 х 5 ³ 10,
2 х 1 + 2 х 2 + 4 х 3 + 6 х 4 + 2 х 5 ³ 40,
х 1³ 0 х 2³0, х 3³ 0 х 2³0, х 5³ 0.
Порядок виконання роботи
1. Відвести комірки А3:E3 під значення змінних хi i =1,2,…,5.
2. Ввести в комірку С4 функцію цілі (як формулу):
=12*А3 + 36*B3 + 32*C3 + 18*D3 + 10*E3.
3. Ввести в комірки діапазону А7:А10 ліві частини обмежень, а в комірки В7:В10діапазону відповідні праві частини обмежень (табл.5.6).
Таблиця 5.6 – Дані для введення обмежень в задачі про суміші
| Комірка | Формула | Комірка | Значення |
| А7 | =2*А3 + 12*B3 + 10*C3 + 1*D3 + 2*E3 | В7 | |
| А8 | =12*А3 + 0*B3 + 0*C3 + 4*D3 + 3*E3 | В8 | |
| А9 | =1*А3 + 8*B3 + 3*C3 + 0*D3 + 4*E3 | В9 | |
| А10 | =2*А3 + 2*B3 + 4*C3 + 6*D3 + 2*E3 | В10 |
На рис.5.2 наведено результат введення даних на робочий лист.

Рисунок 5.2 – Робочий лист з вхідними даними задачі
4. Комірку С4, де знаходиться цільова функція, треба виділити і звернутися до меню СЕРВИС/ПОИСК РЕШЕНИЯ (рис.5.3).
У вікні діалогу вказується цільова комірка С4. В групі РЕЗУЛЬТАТ вибирається кнопка МИНИМАЛЬНОЕ ЗНАЧЕНИЕ, в групі ПУТИ ИЗМЕНЕНИЯ ЯЧЕЙКИ – $А$3:$Е$3. В групі ОГРАНИЧИТЕЛЬНЫЕ УСЛОВИЯ у вікні ССЫЛКА НА ЯЧЕЙКУ вказується діапазон $А$7:$А$10 та обирається операція ³, значення $В$7:$В$10, вказується діапазон $А$7:$А$10 і обирається операція ³, значення задається рівним 0.
У вікні ПАРАМЕТРЫ (рис. 5.4) встановлюється прапорець ПРИНЯТЬ ПЕРЕМЕННЫЕ КАК НЕОТРИЦАТЕЛЬНІЕ.
Натиснути кнопку РЕШИТЬ. В результаті в діалоговому вікні РЕЗУЛЬТАТ (рис. 5.5) з’явиться інформація про завершення пошуку рішення.
Приклад 2
Задачацілочислової оптимізації (задача про добрива для газонів).
Фірма випускає два пакети добрив для газонів: стандартний і поліпшений. В стандартний пакет входять 3 кг азотних, 4 кг фосфорних та 1 кг калійних добрив, а в поліпшений – 2 кг азотних, 6 кг фосфорних та 2 кг калійних добрив. Відомо, що для конкретного газону потребується щонайменше 10 кг азотних, 20 кг фосфорних и 7 кг калійних добрив. Стандартний пакет коштує 3 у.о., а поліпшений – 4 у.о. Скільки і яких пакетів добрив необхідно купити, щоб забезпечити ефективність ґрунту у газоні і мінімізувати ціну пакета з добривами?
Для розв’язку задачі необхідно сформулювати математичну модель.
Нехай х – кількість стандартних пакетів добрив, у – кількість поліпшених пакетів добрив. Цільова функція в даному випадку така:
f(x, у) = Зх + 4у ® mіn
при обмеженнях:
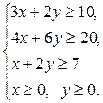

Рисунок 5.3 – Задання обмежень для функції цілі

Рисунок 5.4 – Вікно ПАРАМЕТРЫ для задачі про суміші
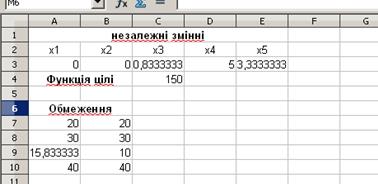
Рисунок 5.5 – Результат розв’язку задачі
Порядок виконання роботи
1 Ввести наступні формули:
в комірку В7 функцію із категорії МАССИВ
= SUMPRODUCT (B3:B4, $F$3:$F$4) – В6;
формулу скопіювати в C7:D7;
в комірку Е7
=SUMPRODUCT(E3:E4;$F$3:$F$4).
Вікно з вхідними даними задачі наведено на рисунку 5.6.
2 В комірці Е7 знаходиться цільова функція. Цю комірку треба виділити і звернутися до меню СЕРВИС/ПОИСК РЕШЕНИЯ.
У вікні діалогу вказується цільова комірка Е7. В групі РЕЗУЛЬТАТ вибирається кнопка МИНИМАЛЬНОЕ ЗНАЧЕНИЕ, в групі ПУТИ ИЗМЕНЕНИЯ ЯЧЕЙКИ – $F$3:$F$4. В групі ОГРАНИЧИТЕЛЬНЫЕ УСЛОВИЯ у вікні ССЫЛКА НА ЯЧЕЙКУ вказується діапазон $B$7:$D$7, обирається операція ³, значення задається рівним 0.
У вікні ПАРАМЕТРЫ (рис. 5.6) встановлюється прапорець ПРИНЯТЬ ПЕРЕМЕННЫЕ КАК ЦЕЛОЧИСЛЕННЫЕ.
3 Натиснути кнопку РЕШИТЬ. В результаті в діалоговому вікні РЕЗУЛЬТАТ (рис.5.7) з’явиться інформація про завершення пошуку рішення.
Таблиця 5.7 – Дані для оптимізаційної задачі
| А | В | С | D | Е | F |
| Азотні | Фосфорні | Калієві | Ціна | Кількість | |
| Стандартний пакет | |||||
| Поліпшений пакет | |||||
| Потрібно >= | Загальна ціна: | ||||
| Обмеження | -10 | -20 | -7 |

Рисунок 5.6– Вікно з вхідними даними задачі

Рисунок 5.7– Діалогове вікно РЕЗУЛЬТАТ
На робочому листі (рис.3.8) представлені результати розв’язання задачі цілочислової оптимізації.
. 
Рисунок 5.8 – Результат розв’язання задачі цілочислової оптимізації
Контрольні запитання
1. Як формулюється задача оптимізації?
2. Назвіть основні типи оптимізаційних задач.
3. Як розв’язати задачу лінійного програмування в OpenOffice.org Calc?
4. Опишіть діалогове вікно ПОИСК РЕШЕНИЯ.
5. Як задати обмеження в задачі оптимізації?
6. Опишіть діалогові вікна ПАРАМЕТРЫ і РЕЗУЛЬТАТ.
СПИСОК ДЖЕРЕЛ ІНФОРМАЦІЇ
1 Бахвалов Н.С. Численные методы/ Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.– М.: Бином Лаборатория знаний, 2008. – 536 с.
2 Демидович Б.П. Основы вычислительной математики /Б.П.Демидович, И.А. МАрон. –Спб.: Лань, 2011.– 672 с.
3 Ляшенко Б.М., Кривонос О.М., Вакалюк Т.А. Методи обчислень: навчально-методичний посібник. – Житомир: Вид-во ЖДУ, 2014.– 228 с.
4 Питоньяк Э. OpenOffice.org. Автоматизация работы. – М.:«ДМК Пресс», 2009. - 512 с.
5 OpenOffice.org. Руководство по Calc.– М.: Инфра Ресурс, 2007.– 254 с.
6 Новожилова М.В., Сізова Н.Д., Петрова О,О, Н.В. Гречко Н.В. «MS EXCEL 2010. Лабораторний практикум. Частина 1. «Обробка і аналіз даних»».– Харків: ХНУБА, 2013.– 140 с.
7 Новожилова М.В., Сізова Н.Д., Петрова О,О, Н.В. Гречко Н.В. «MS EXCEL 2010.Лабораторний практикум. Частина 2. «Автоматизація фінансових розрахунків та деякі задачі математичної статистики й математичного програмування»».– Харків: ХНУБА, 2013.– 208 с.
Сізова Н.Д., Петрова О.О., Гречко Н.В. Вбудовані функції MathCad для розв’язання математичних задач будівельної механіки. Навчально-методичний посібник. – Харків: ХНУБА, 2016. –95 с.
ЗМІСТ
ВСТУП.. 3
ЛАБОРАТОРНА РОБОТА № 1. 4
ОБРОБКА ТАБЛИЧНИХ ДАНИХ З ВИКОРИСТАННЯМ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ.. 4
ЛАБОРАТОРНА РОБОТА № 2. 23
ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ З З ВИКОРИСТАННЯМ ЛІНІЙ ТРЕНДА 23
ЛАБОРАТОРНА РОБОТА № 3. 29
РЕГРЕСІЙНИЙ АНАЛІЗ ДЛЯ ПОБУДОВИ МОДЕЛІ ЗА ЕКСПЕРИМЕНТАЛЬНИМИ ДАНИМИ.. 29
ЛАБОРАТОРНА РОБОТА № 4. 39
ПРОГНОЗУВАННЯ З ВИКОРИСТАННЯМ ВБУДОВАНИХ ФУНКЦІЙ.. 39
ЛАБОРАТОРНА РОБОТА № 5. 47
ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ ЗАСОБАМИ.. 47
ЛІНІЙНОГО ПРОГРАМУВАННЯ.. 47
СПИСОК ДЖЕРЕЛ ІНФОРМАЦІЇ 60






