ВСТУП
В багатьох питаннях, пов’язаних з роботою будівельної галузі, необхідним моментом є проведення натурних експериментів, що дозволяє прийняти відповідні рішення з експлуатації конкретних елементів і впровадження нових матеріалів.
Експериментальні дослідження дають можливість вивчити реальні явища чи процеси в роботі того чи іншого об’єкта. Але натурні експерименти не завжди прийнятні, наприклад, у випадках, коли фізичні розміри компонентів об’єкта достатньо малі, або не має можливості встановити високо точні прилади і датчики. Крім того, натурні експерименти потребують значних фінансових витрат і часу на їх проведення, інформаційної обробки одержаних даних.
Тому актуальним є визначення необхідних характеристик об’єкта, що досліджується, аналітичними і чисельними методами. Аналітичні підходи до рішення конкретної проблеми можливі для обмеженого числа задач.
Для широкого класу задач прийнятним є використання чисельних методів [1-3] і створених на їх основі програмних комплексів і пакетів, тобто використання сучасних інформаційних технологій і обчислювального експерименту [4-7].
Рішення задачі визначення необхідних параметрів дозволяє на стадії обчислювального експерименту одержувати достовірну і об’єктивну інформацію про роботу конструктивного елемента, частково або повністю замінити експериментальні досліди розрахунковим проектуванням, прогнозувати фізичні процеси, розраховувати оптимальні параметри роботи всієї конструкції.
В методичних вказівках подається матеріал з обробки експериментальних даних. В ньому приводяться основні підходи, пов’язані з використанням числових методів обробки результатів, зокрема, інтерполяційні поліноми, регресійний аналіз. Крім того, представлена можливість використання програмних пакетів для аналізу, прогнозування та оптимізації експлуатаційних параметрів об’єктів.
Дані методичні вказівки призначено для формування у студентів будівельних спеціальностей навичок в області застосування інформаційних технологій, методів математичного і комп’ютерного моделювання в задачах будівництва
Запропоновані в даному виданні роботи рекомендується виконувати з застосуванням сучасних програмних пакетів і комплексів, або з розробкою індивідуальних програм на одній з мов програмування [4-7,8].
.
ЛАБОРАТОРНА РОБОТА № 1
ОБРОБКА ТАБЛИЧНИХ ДАНИХ З ВИКОРИСТАННЯМ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ
Мета – обробка експериментальних даних з використанням інтерполяційних поліномів
Завдання до виконання роботи
1 Побудувати відповідно до індивідуального варіанта (табл. 1.1) за табличними даними інтерполяційні поліноми інтерполяційний поліном Лагранжа, сплайни лінійний і квадратичний.
2 Знайти методом найменших квадратів емпіричну формулу для даних експерименту (табл. 1.2).
Таблиця 1.1 – Значення функції в точках для побудови інтерполяційного поліному
| Номер варіанта | Значення функції в точках | |||||
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 3,03 | 3,14 | 3,35 | 3,46 | 3,77 | |
| х | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | |
| у | 6,71 | 6,73 | 6,75 | 6,74 | 6,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 2,32 | 2,51 | 2,63 | 2,70 | 2,69 | |
| х | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| у | 1,04 | 1,16 | 1,26 | 1,17 | 1,07 | |
| х | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | |
| у | 1.75 | 1,76 | 1,77 | 1,79 | 1,82 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 2,03 | 2,14 | 2,35 | 2,46 | 2,77 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 6,71 | 6,73 | 6,75 | 6,74 | 6,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 2,32 | 2,51 | 2,63 | 2,70 | 2,69 | |
| х | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| у | 1,94 | 1,96 | 1,92 | 1,87 | 1,97 | |
| х | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | |
| у | 2.75 | 2,76 | 2,77 | 2,79 | 2,82 |
Продовження табл. 1.1
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 3,3 | 3,14 | 3,55 | 3,46 | 3,07 | |
| х | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | |
| у | 1,71 | 1,73 | 1,75 | 1,74 | 1,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 3,32 | 3,51 | 3,63 | 3,70 | 3,69 | |
| х | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| у | 2,04 | 2,16 | 2,26 | 2,17 | 2,07 | |
| х | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | |
| у | 1.05 | 1,06 | 1,07 | 1,09 | 1,22 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 2,03 | 2,14 | 2,35 | 2,46 | 2,77 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 3,71 | 3,73 | 3,75 | 3,74 | 3,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 2,52 | 2,61 | 2,73 | 2,82 | 2,78 | |
| х | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| у | 1,94 | 1,96 | 1,92 | 1,87 | 1,97 | |
| х | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | |
| у | 2.75 | 2,76 | 2,77 | 2,79 | 2,82 | |
| х | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| у | 1,94 | 1,96 | 1,92 | 1,87 | 1,97 | |
| х | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | |
| у | 2.75 | 2,76 | 2,77 | 2,79 | 2,82 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 3,3 | 3,14 | 3,55 | 3,46 | 3,07 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 3,03 | 3,14 | 3,35 | 3,46 | 3,77 | |
| х | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | |
| у | 6,71 | 6,73 | 6,75 | 6,74 | 6,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 2,32 | 2,51 | 2,63 | 2,70 | 2,69 | |
| х | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | |
| у | 1.75 | 1,76 | 1,77 | 1,79 | 1,82 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 2,03 | 2,14 | 2,35 | 2,46 | 2,77 | |
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 6,71 | 6,73 | 6,75 | 6,74 | 6,64 | |
| х | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| у | 2,03 | 2,14 | 2,35 | 2,46 | 2,77 |
Таблиця 1.2 – Варіанти функції для лінійної і квадратичної апроксимації
| Номер варіанта | Значення функції в точках | |||||||
| х | ||||||||
| у | 0,2 | 0,6 | 1,0 | 1,2 | 1,3 | 1,6 | 1,8 | |
| х | -2 | -1 | ||||||
| у | 3,1 | 2,8 | 2,5 | 2,0 | 1,7 | 2,2 | 2,9 | |
| х | -6 | -4 | -3 | -1 | ||||
| у | 2,5 | 1,2 | 0,4 | -0,5 | -1,3 | -1,2 | 1,1 | |
| х | ||||||||
| у | 0,5 | 0,8 | 1,3 | 1,7 | 1,9 | 2,5 | 2,2 | |
| х | -3 | -2 | ||||||
| у | 1,7 | 1,2 | 1,0 | 0,5 | -0,2 | 0,5 | 0,8 | |
| х | ||||||||
| у | 2,1 | 2,2 | 2,3 | 2,4 | 2,6 | 2,5 | 2,4 | |
| х | -1 | -2 | ||||||
| у | -1,8 | -1,5 | -1,1 | -1,3 | -1,4 | -1,6 | -1,9 | |
| х | -4 | -3 | -1 | |||||
| у | 1,0 | 1,7 | 3,3 | 5,1 | 4,6 | 3,0 | 1,9 | |
| х | ||||||||
| у | 3,1 | 3,3 | 3,4 | 3,7 | 3,2 | 2,9 | 1,1 | |
| х | -2 | -1 | ||||||
| у | -0,3 | 0,5 | 0,8 | 1,8 | 0,8 | 0,4 | 0,0 | |
| х | ||||||||
| у | 1,8 | 1,9 | 2,3 | 2,5 | 2,8 | 3,1 | 2,5 | |
| х | -2 | -1 | ||||||
| у | 0,3 | -0,5 | -1,5 | -0,5 | -0,1 | -0,2 | 1,2 | |
| х | -3 | -2 | -1 | |||||
| у | 4,8 | 4,2 | 3,7 | 3,6 | 3,3 | 3,1 | 2,8 | |
| х | ||||||||
| у | 3,5 | 3,2 | 2,9 | 2,1 | 3,0 | 3,2 | 3,5 | |
| х | -1 | |||||||
| у | -6,1 | -5,8 | -5,2 | -4,8 | -4,5 | -5,0 | -5,2 | |
| х | -2 | -1 | ||||||
| у | 1,1 | 0,2 | -0,4 | -1,0 | -1,1 | -1,0 | -0,2 | |
| х | ||||||||
| у | -1,2 | -0,5 | -0,2 | 0,3 | 0,7 | 1,1 | 1,4 | |
| х | ||||||||
| у | 1,8 | 1,2 | 0,2 | -0,9 | -1,9 | 0,4 | 2,4 |
Продовження табл.1.2
| х | -2 | -1 | ||||||
| у | 1,7 | 1,9 | 2,4 | 2,7 | 3,1 | 3,1 | 2,5 | |
| х | -1 | -2 | ||||||
| у | -1,8 | -1,5 | -1,1 | -1,3 | -1,4 | -1,6 | -1,9 | |
| х | -4 | -3 | -1 | |||||
| у | 1,0 | 1,7 | 3,3 | 5,1 | 4,6 | 3,0 | 1,9 | |
| х | ||||||||
| у | 3,1 | 3,3 | 3,4 | 3,7 | 3,2 | 2,9 | 1,1 | |
| х | -2 | -1 | ||||||
| у | -0,3 | 0,5 | 0,8 | 1,8 | 0,8 | 0,4 | 0,0 | |
| х | ||||||||
| у | 1,8 | 1,9 | 2,3 | 2,5 | 2,8 | 3,1 | 2,5 | |
| х | -2 | -1 | ||||||
| у | 0,3 | -0,5 | -1,5 | -0,5 | -0,1 | -0,2 | 1,2 | |
| х | -1 | |||||||
| у | 3,1 | 2,8 | 2,4 | 2,1 | 1,9 | 2,2 | 2,6 | |
| х | -2 | -1 | ||||||
| у | 3,1 | 2,8 | 2,5 | 2,0 | 1,7 | 2,2 | 2,9 | |
| х | -6 | -4 | -3 | -1 | ||||
| у | 2,5 | 1,2 | 0,4 | -0,5 | -1,3 | -1,2 | 1,1 | |
| х | ||||||||
| у | 0,5 | 0,8 | 1,3 | 1,7 | 1,9 | 2,5 | 2,2 | |
| х | -3 | -2 | ||||||
| у | 1,7 | 1,2 | 1,0 | 0,5 | -0,2 | 0,5 | 0,8 |
Загальні положення
На практиці часто необхідно розв’язати задачу – побудувати плавну криву для експериментальних даних, тобто треба розв’язати задачу апроксимації.
Апроксимацією називається процес вибору емпіричної формули j(x) для функції y=f(x), одержаної із досліду, тобто. знаходження такої функції, яка найточніше описує функцію, задану у вигляді таблиці, тобто заміну функції f(x) функцією φ (x), близькою до першої. Емпіричні формули дають аналітичне представлення даних досліду.
Якщо наближення виконується на заданому дискретному інтервалі множень точок{ xi }, то таку апроксимацію називають точковою. При побудові наближення на неперервній множині точок, наприклад, на відрізку[ a, b ], апроксимація називається неперервною або інтегральною.
Розглянемо задачу апроксимації для однієї змінної.
Як правило, задача апроксимації розпадається на дві частини.
Спочатку встановлюється вид залежності y=f(x), тобто вид емпіричної формули, яка може бути лінійною, квадратичною, логарифмічною або якоюсь іншою. Після цього визначають чисельні значення невідомих параметрів обраної емпіричної формули, для яких наближення до заданої функції є найкращим. Для найкращого вибору параметрів задають міру наближення апроксимації експериментальних даних. Звичайно визначення параметрів, якщо відомий вид функціональної залежності, відбувається з використанням методу найменших параметрів. При цьому функція j(x) є найкращим наближенням до f(x), якщо сума квадратів нев’язок di або відхилень “теоретичних значень” значень j(xi), знайдених за емпіричною формулою, від відповідних даних досліду значень yi,
має найменше значення в порівнянні з іншими функціями, з числа яких обирається наближення, що відшукується.
Нехай y = ax + b, тоді метод найменших квадратів дає таку систему для визначення коефіцієнтів a, b:
Інтерполяція. Типи інтерполяції.
Одним із основних типів точкової апроксимації є інтерполяція.
Найпростіша задача інтерполяції полягає в такому: на відрізку задані точки, які називаються вузлами інтерполяції, і значення деякої функції у цих точках.
Необхідно побудувати таку функцію (так звану інтерполяційну функцію), яка приймає у вузлах інтерполяції ті самі значення, що й функція. Тобто треба знайти криву певного типу, що проходить через задану систему точок. Знайшовши таку функцію, ми зможемо знайти її значення в кожній точці відрізку. Можна дати таке визначення інтерполяції.
Інтерполяція – це спосіб знаходження проміжних значень функції за дискретним набором відомих значень.
Інтерполяція за допомогою полінома називається параболічною.
Точки x 0, x1, x2,..., xn, в яких функція має значення y0, y1, y2,..., yn, називають вузлами інтерполяції.
Якщо між різними вузлами поліноми різні, то така інтерполяція називається локальною.
Якщо поліном один для всього інтервалу інтерполяції, то така інтерполяція називається глобальною.
Процес побудови послідовності інтерполяційних поліномів по послідовності сіток, що згущаються, на 
називається інтерполяційним процесом.
За допомогою полінома можна знаходити значення функції у вузлах, які знаходяться за межами інтервалу. В такому випадку процес знаходження значень функції називають екстраполяцією.
Якщо задані значення функції в двох вузлах x0 та x 1 і ці значення дорівнюють y0 та y 1, то лінійну функцію на відрізку можна записати формулою:
y = Ax + B,
в якій при x=x0 , y=y0, а при x=x1 y=y1. Це – лінійна інтерполяція
Якщо задані значення функції в трьох вузлах x0, x1 та x 2 і ці значення дорівнюють y0, y1 та y 2, то інтерполяційний поліном буде мати вигляд параболи, яку можна описати рівнянням виду:
y = Ax2 + Bx + C.
Квадратична інтерполяція представляється формулою:
Якщо задані значення функції в чотирьох вузлах x0, x1, x2 та x 3 і ці значення дорівнюють y0, y1, y2 та y 3, то інтерполяційний поліном буде мати вигляд кубічної параболи, яку можна описати рівнянням виду:
y = Ax3 + Bx2 + Cx + D.
Це – кубічна інтерполяція, яку можна записати формулою:
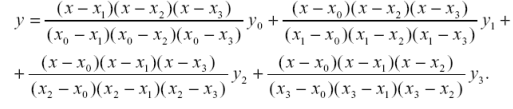
Результати експериментів завжди мають якусь похибку і ця похибка часто буває досить великою. В таких випадках інтерполяційна крива не буде відповідати справжній залежності. Подібні ситуації виникають доволі часто, тому інтерполяція рідко використовується при аналізі результатів експериментів.
Інтерполяційний поліном Лагранжа. Сплайни.
Для функції, яка задана таблицею, можна побудувати інтерполяційні поліноми.
Якщо на відрізку [ a, b ] задано вузли інтерполювання хк (k =0,1, …, n) і значення функції f (x) в цих вузлах
| х | х 0 | х 1 | … | хn |
| f(х) | f(х 0) | f (х 1) | … | f(хn) |
то можна побудувати інтерполяційний поліном, тобто поліном, степені не вище n, значення якого у вузлах інтерполяції співпадають з заданими значеннями функції.
Інтерполяційний поліном Лагранжа в загальному випадку для n + 1вузлів (точок)має вигляд:
.
Процес побудови послідовності інтерполяційних поліномів по послідовності сіток, що згущуються, на 
називається інтерполяційним процесом.
Одним зі способів інтерполяції на усьому відрізку є інтерполяція за допомогою сплайнів. Перевагою сплайнів перед звичайною інтерполяцією є, по-перше, їхня збіжність, і, по-друге, стійкість процесу обчислень.
Слово,,сплайн’’ (англ. spline) означає гнучку лінійку, яка використовується для проведення гладких кривих через задані точки площини.
Нехай обрані цілі числа m ³0 і l ³-1 та на інтервалі задано сітку.
Сплайном степені m гладкості l називається функція sm,l(x), яка задовольняє двом умовам:
на кожному з інтервалів [ xi, xi +1] вона є алгебраїчним поліномом ступеня не вище m, тобто Sm,l (f, x)= Pim (x)= ai 0+ ai 1+…+ aimxm, i =1,… n (n – кількість розбивок);
на всьому інтервалі 
вона належить класові гладкості Cl , тобто її похідні неперервні в точках xi порядку l- 1. (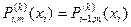
, де xi – заданий вузол, i =1,… n -1; k =0,…, m -1).
Звичайно вибирають l = m. Якщо будувати сплайн m -го порядку, то невідомих (m +1) n. Можна будувати сплайни будь-якого порядку.
Сплайн першого порядку називається лінійним (інтерполяційний)
Відрізків n, на кожнім відрізку дві невідомих, значить всього 2 n невідомих. Оскільки функція неперервна, тоб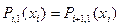то 
, то
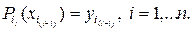
Значення коефіцієнтів наступні:
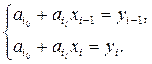
Звідки коефіцієнти
.
Система MathCad дозволяє проводити інтерполяцію набору експериментальних точок. Для цього в системі є функції, які дають можливість інтерполювати функцію різними методами. Сплайни можуть бути поліномами 1,2,3 степені (лінійні, квадратичні, кубічні).
Для інтерполяції з використанням сплайнів можна звернутися до програмного пакету MathCad [8], який має наступні вбудовані функції.
Функція lspline (vx,vy) інтерполює функцію, що задана таблицею. У начальній і кінцевій точках накладається умова лінійності, тобто друга похідна функції дорівнює нулю. Перша буква в назві функції l означає лінійний (linear).
Функція рspline (vx,vy) інтерполює функцію, що задана таблицею, таким чином, що на першому і останньому інтервалі крива є параболою, тобто поліноміальний коефіцієнт при х 3 дорівнює нулю. Перша буква в назві функції р означає параболічний (parabolic).
Функція сspline (vx,vy) інтерполює функцію, що задана таблицею, таким чином, що на перших двох інтервалах, а також на останніх двох інтервалах поліноміальні коефіцієнти при х 3 рівні між собою. Перша буква в назві функції с означає кубічний (cubic).
Результатом кожної функції є вектор, в якому є значення других похідних від інтерполяційної кривої у всіх точках, які задані в масиві vx.
Для того, щоб побудувати з цього вектора криву, необхідно скористатися вбудованою функцією interp (v, vx,vy,x), де vx і vy – масиви експериментальних точок, v – масив, який отримано як результат однієї з трьох функцій, х – координата, в якій визначається значення інтерполяційної кривої.
Таким чином, сплайнова інтерполяція в MathCad відбувається в два етапи. На першому етапі визначається вектор похідних при допомозі однієї з трьох функцій lspline, рspline, сspline, на другому визначається інтерполяційна залежність за допомогою функції interp.
Функція interp апроксимуєдані функції за допомогою В–сплайнів.
B(vx,vy,u,n) – вектор значень коефіцієнтів В – сплайна; u – вектор значень аргументу, в яких проводиться зшивання В – сплайнів, n – порядк сплайнової інтерполяції (1,2,3). Розмірність вектора u повинна бути на 1,2 або 3 менше розмірності векторів vx і vy. Перший елемент вектора u має бути менше або дорівнювати першому елементу вектора vx, а останній елемент – більше або дорівнювати останньому елементу vx.
Інтерполяція В–сплайнами – складніший тип інтерполяції. На відміну від звичайної сплайн-інтерполяції, зшивання елементарних В–сплайнів проводиться не в точках vx, а в інших точках вектору u, які вибираються довільно із відрізка, на якому задано експериментально значення функції.
