Що означає ступінь детермінації?

 

 

Рисунок 2.2 – Контекстне меню для лінії тренда

 

 

Рисунок 2.3 – Графіки, які апроксимують функцію задану таблицею

Контрольні питання

 

1 Дайте визначення апроксимації.

2 Опишіть алгоритм побудови лінії тренда.

Що означає ступінь детермінації?

 

 

ЛАБОРАТОРНА РОБОТА № 3

РЕГРЕСІЙНИЙ АНАЛІЗ ДЛЯ ПОБУДОВИ МОДЕЛІ ЗА ЕКСПЕРИМЕНТАЛЬНИМИ ДАНИМИ

Мета роботи – використання регресійного аналізу для побудови регресійної моделі для даних, що задані таблицею

Завдання для підготовки до виконання роботи

 

1 Побудувати парну лінійну регресійну модель за даними, що наведено у таблиці 3.1. Зв’язок між даними являється лінійним.

2 Обчислення провести двома способами: з використанням вбудованих статистичних функцій і функцій масиву

 

Таблиця 3.1 – Вхідні дані

 

	Х
У
	Х
У
	Х		12,5		13,5		14,5		15,5		16,5
У				9,8		9,5	9,5	9,2	8,6	8,3
	Х
У	1,1	1,07	1,05	0,98		0,95	0,97	0,92	0,8	0,9
	Х
У
	Х
У
	У
Х		12,5		13,5		14,5		15,5		16,5
	У				9,8		9,5	9,5	9,2	8,6	8,3
Х
	У	1,1	1,07	1,05	0,98		0,95	0,97	0,92	0,8	0,9
Х
	У
У
	Х
Х
	У
Х		12,5		13,5		14,5		15,5		16,5
	У				9,8		9,5	9,5	9,2	8,6	8,3
Х
	У	1,1	1,07	1,05	0,98		0,95	0,97	0,92	0,8	0,9
Х
	У
У

 

 

Продовження табл. 3.1

 

	Х
У
	Х
У
	Х
У
	Х
У
	Х
У		20,7	20,5	19,8	19,5	20,5	19,5	19,2	19,6	19,3
	Х
У
	Х
У	2,1	2,4	2,5	1,9	2,5	1,8	1,9	1,7	1,8	1,6
	У
Х		12,5		13,5		14,5		15,5		16,5
	У				9,8		9,5	9,5	9,2	8,6	8,3
Х
	У	1,1	1,07	1,05	0,98		0,95	0,97	0,92	0,8	0,9
Х
	У
У
	Х
У
	Х
У
	Х
У
	Х
У

Загальні положення

Регресійний аналіз використовується для визначення рівняння, яке описує експериментальну залежність в дослідах. Метою аналізу є одержання формули кривої на основі експериментальних даних за допомогою методу найменших квадратів.

Регресія може бути лінійною або нелінійною. Вибір виду регресії базується як на кількості і якості експериментальних даних, так і теоретичних припущеннях.

У випадку одномірної регресії Y=f(x), коли є набір експериментальних точок (x_i,y_i) в площині ХУ і необхідно одержати вигляд функції f(x), використовується метод найменших квадратів. За методом найменших квадратів необхідно підібрати коефіцієнти в рівнянні f(x) таким чином, щоб сума квадратів відхилень по у при всіх х була мінімальною, тобто необхідно мінімізувати функціонал

,

де n – кількість експериментальних точок, f(x_i) – теоретичне значення функції в точці х _i, у _i – експериментальне значення.

Нехай змінна Х приймає деякі фіксовані значення х ₁, х ₂,… х_n. Відповідні значення залежної змінної У мають діапазон внаслідок похибки вимірювань і різних факторів, що не були враховані, і дорівнюють у ₁, у ₂,…, у_n.

Якщо припустити, що зв’язок між змінним є лінійним, то відповідна регресійна модель має вигляд:

,

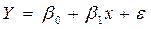де b ₀, b ₁ – параметри лінійної регресії, e – випадкова похибка спостережень.

Припускається, що математичне сподівання М(e)=0, а дисперсія D(e) є постійною.

Задача регресійного аналізу зводиться до оцінки параметрів регресії b ₀, b ₁, перевірки гіпотези про значимість моделі і оцінці її адекватності, тобто достатньо добре чи ні співпадає модель з результатами спостережень.

Для оцінки параметрів моделі використовується метод найменших квадратів: в якості оцінок приймаються такі значення b ₀, b ₁, які мінімізують суму квадратів відхилень значень у_i, що спостерігаються, від розрахункових точок .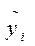

Для парної лінійної моделі ці оцінки визначаються за формулами:

де

,

.

Розрахункове значення (прогноз) обчислюється за формулою

.

Різниця між значеннями, що спостерігаються, і розрахунковими значеннями називається залишками, а відповідна сума квадратів – залишковою сумою квадратів:

.

Лінійна регресійна модель називається незначущою, якщо параметр b ₁ =0.

Для перевірки відповідної нульової гіпотези використовується статистика Фішера:

,

які при заданому рівні значущості a порівнюється з квантиллю з числом ступенів свободи 1 і (n -2). Якщо F > , то нульова гіпотеза відкидається, це значить, що регресійна модель статистично значуща.

Для характеристики якості тієї чи іншої моделі може використовуватися коефіцієнт детермінації – квадрат коефіцієнта кореляції між досліджуваними і прогнозними значеннями

.

Чим ближче коефіцієнт детермінації до 1, тим більш якісною вважається модель.

Найбільш поширеними є наступні види функції f(x) (моделі):

1) лінійна модель f(x)= ах+b;

2) показова функція f(x)= аb^x (або c*exp(d*x));

3) степенева функція f(x)= ах^b;

4) логарифмічна модель f(x)= а*log(x).

Якщо задано вигляд функції і визначені коефіцієнти, то модель побудовано. Після побудови моделі необхідно перевірити її адекватність, тобто застосування її для діапазонів значень х, які раніше не були досліджувані.

Продовження функції за границі проміжку, що досліджується називається екстраполяцією, а одержання значень всередині проміжку між експериментальними точками – інтерполяцією.

В разі продовження залежності за границі точок дослідження ця залежність не повинна проявляти екстремальну поведінку.

Для проведення регресійного аналізу в OpenOffice.org Calc використовуються як статистичні функції, так і функції масиву.

Серед статистичних функцій чотири функції призначені для розрахунку парної регресії:

обчислення коефіцієнтів b ₀ – INTERCEPT;

обчислення коефіцієнтів b _1­ – SLOPE;

розрахунку прогнозних значень – FORECAST;

визначення коефіцієнта детермінації RSQ.

За допомогою функції INTERCEPT (рис.3.1) обчислюються координати для точок перетину лінії з віссю у за допомогою відомих значень х і у. Синтаксис цієї функції наступний

INTERCEPT (ВХІДНІ_У; ВХІДНІ_Х),

де ВХІДНІ_У – залежна множина спостережень або даних; ВХІДНІ_Х – незалежна множина спостережень або даних.

Як аргументи можна використовувати імена, масиви або посилання, які мають числа. Можна також вводити числа.

Функція SLOPE обчислює тангенс кута лінії регресії. Синтаксис цієї функції наступний:

SLOPE (ВХІДНІ_У; ВХІДНІ_Х),

де ВХІДНІ_У – масив або матриця даних У; ВХІДНІ_Х – масив або матриця даних Х.

Функція FORECAST обчислює майбутні значення по існуючим значенням х і у.

Синтаксис цієї функції наступний

FORECAST (ЗНАЧЕННЯ; ВХІДНІ_У; ВХІДНІ_Х),

де ЗНАЧЕННЯ – значення Х, для якого обчислюється значення лінійної регресії; ВХІДНІ_У – масив або діапазон даних У; ВХІДНІ_Х – масив або діапазон даних Х.

 

 

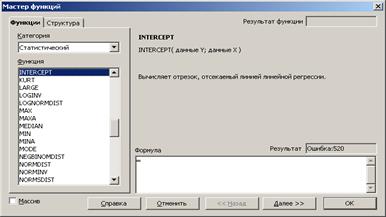
Рисунок 3.1 – Вбудована функція INTERCEPT

 

Функція RSQ повертає квадрат коефіцієнта кореляції Пірсона для вказаних значень. RSQ (коефіцієнт кореляції) характеризує ступінь точності корегування, яка використовується для аналізу регресії.

Синтаксис цієї функції наступний

RSQ (ВХІДНІ_У; ВХІДНІ_Х),

де ВХІДНІ_У – масив або діапазон точок даних У; ВХІДНІ_Х – масив або діапазон точок даних Х.

Друга група функцій, які призначені для проведення регресійного аналізу, це функції масиву. Ці функції можуть бути використані як для проведення парної регресії, так і для нелінійної і множинної регресії. Це такі функції:

LINEST – лінійна регресія;

TREND – прогноз по лінійній регресії;

LOGEST – експоненціальна регресія;

GROWTH – прогноз по експоненціальній регресії.

Функція LINEST (рис.2.2) повертає параметри лінійного тренда. Синтаксис цієї функції наступний:

LINEST (ВХІДНІ_У; ВХІДНІ_Х; Тип_ЛІНІІ; СТАТИСТИКА),

де ВХІДНІ_У – масив даних У; ВХІДНІ_Х – масив даних Х; Тип_ЛІНІІ (необов’язково) – якщо лінія проходить через 0, то його треба вказати; СТАТИСТИКА (необов’язково) – якщо для цього параметра вказано 0, то обчислюється коефіцієнт регресії, в інших випадках відображаються інші дані (рис. 3.2).

 

 

Рисунок 3.2 – Вбудована функція LINEST

 

Функція TREND повертає значення по лінійному тренду. Синтаксис цієї функції наступний:

TREND (ВХІДНІ_У; ВХІДНІ_Х; НОВІ_ДАНІ_Х; Тип_ЛІНІІ),

де ВХІДНІ_У – масив даних У; ВХІДНІ_Х – масив даних Х; НОВІ_ДАНІ_Х (необов’язково) – масив даних Х, які використовуються для повторного обчислення значень; Тип_ЛІНІІ (необов’язково) – якщо дорівнює 0, то лінії проходять через початок координат, в іншому випадку розраховуються зміщені лінії.

Функція LOGEST служить для розрахунку корегування для введених даних у вигляді кривої експоненціальної регресії (y = bm^x). Синтаксис цієї функції наступний

LOGEST (ВХІДНІ_У; ВХІДНІ_Х; Тип_ФУНКЦІІ; СТАТИСТИКА),

де ВХІДНІ_У – масив даних У; ВХІДНІ_Х – масив даних Х; Тип_ФУНКЦІІ (необов’язково) – якщо цей параметр дорівнює 0, то функція приймає форму y = m^x, в іншому випадку – y = bm^x); СТАТИСТИКА (необов’язково) – якщо для цього параметра вказано 0, то обчислюється коефіцієнт регресії.

Функція GROWTH розраховує точки експоненціального тренда в масиві.

Синтаксис цієї функції наступний:

GROWTH (ВХІДНІ_У; ВХІДНІ_Х; НОВІ_ДАНІ_Х; Тип_ФУНКЦІІ),

де ВХІДНІ_У – масив даних У; ВХІДНІ_Х – масив даних Х; НОВІ_ДАНІ_Х (необов’язково) – масив даних Х, які використовуються для повторного обчислення значень; Тип_ФУНКЦІІ (необов’язково) – якщо цей параметр дорівнює 0, то функція приймає форму y = m^x, в іншому випадку – y = bm^x);

 

Приклад 1

1 Побудувати парну лінійну регресійну модель за даними, що наведено у таблиці 2.1. Зв’язок між даними являється лінійним.

2 Обчислення провести двома способами: з використанням вбудованих статистичних функцій і функцій масиву (рис. 3.2).

 

Таблиця 3.2 – Дані вимірювань

 

Х
У

 

Порядок виконання роботи

 

1 Ввести в діапазон А3:А12 значення Х, в діапазон В3:В12 – У. Зробити відповідні підписи (рис.3.3).

2 Розташувати прогнозовані дані лінійної регресії в діапазоні С3:С12. Для цього ввести в комірку С3 формулу

=FORECAST(A3;$B$3:$B$12;$A$3:$A$12),

скопіювати її до комірки С12.

3 Визначити функції регресії в комірках В15, В16, С16 через вбудовані функції:

=INTERCEPT(B3:B12;A3:A12)

=SLOPE(B3:B12;A3:A12)

=RSQ(B3:B12;A3:A12).

Зробити відповідні підписи.

4. Використати функції масиву для визначення коефіцієнтів в рівнянні регресії.

4.1 В комірку А19 ввести формулу {LINEST(B3:B12;A3:A12;1;1)}. Ця формула відобразить наступні дані: в комірках А19 і В19 – значення коефіцієнтів b₀ і b₁; в А20 і В20 – стандартна похибка коефіцієнтів; в А21 і В21 – коефіцієнт детермінації і стандартна похибка регресії;

4.2 Ввести в діапазон Е20:I20 наступний текст

Рівняння регресії у=b0+b1*x у=В15+В16*х; х — довільна точка.

4.3 В декількох довільних точках обчислити за регресійною моделлю прогнозоване значення для функції у.

 

 

Рисунок 3.3 – Результат регресійної моделі для прикладу 1

Приклад 2

Побудувати регресійну модель для прогнозування зміни рівня захворювання органів дихання (У) в залежності від вмісту у повітрі двоокису вуглецю (Х₁) і ступеня загазованості повітря (Х₂) (табл.3.4).

 

Таблиця 3.4 – Дані вимірювань

 

Х1	Х2	У
	1,3
	1,3
1,1	1,4
1,1	1,4
1,1	1,5
1,1	1,5
	1,4
1,2	1,6
1,2	1,7
0,6
0,6
0,7	1,1
0,7	1,15

 

 

Продовження табл. 3.4

 

0,75	1,2
0,7	1,2
0,7	1,3
0,7	1,3
0,8	1,4
0,8	1,4
0,75	1,5
0,8	1,5
0,78	1,5
0,78	1,6
0,8	1,7
0,8	1,8
0,75	1,8
0,78	1,9
0,75	1,9

 

Порядок виконання роботи

 

1. Ввести в діапазон А3:А31 значення Х₁, в діапазон В3:В31– значення Х₂, в діапазон С3:C31 – значення У (рис.2.3).

2. Розташувати прогнозовані дані лінійної регресії в діапазоні.

2.1. Зробити відповідні надписи:

В діапазоні Е33:Н33 – «Функції масиву», в діапазоні Е36:D40 – «Коефіцієнти», «Стандартна похибка коефіцієнтів», «R² і стандартна похибка регресії», «F», «df», «QR» i «Qe». В комірках F35:H35 зробити підписи «b₀», «b₁», «b₂».

2.2. Ввести в комірку F36 формулу

={LINEST(C3:С31;A3:В31;1;1)}.

Відповідні числові дані регресійного аналізу відобразяться в діапазоні F36:H40 (рис.3.4).

2.3. Записати рівняння регресії в комірках B41:D42 як текст

$H$36+$G$36*A3+$F$36*B3.

3. Одержати прогнозні значення для змінних Х1 і Х2, для чого в комірку D3 ввести формулу

=$H$36+$G$36*A3+$F$36*B3

і скопіювати її до D31.

4. Побудувати графік для регресійної моделі для двох змінних Х1 і Х2 за даними У і прогнозу.

Рисунок 3.4 – Результат регресійної моделі для прикладу 2

5. За даними регресійної моделі побудувати графіки окремо для змінної Х1 і змінної Х2 (самостійно).

 

Контрольні запитання

 

1. Дати визначення регресії.

2. Які значення в регресійному аналізі мають математичне сподівання М(e) і дисперсія D(e)?

3. Які оцінки існують в регресійному аналізі?

4. Які функції при проведенні регресійного аналізу використовуються в OpenOffice.org Calc?

ЛАБОРАТОРНА РОБОТА № 4