Как известно из теории p-n- перехода, часть дырок при прохождении слоя объемного заряда эмиттерного перехода теряется на рекомбинацию. Для поддержания этого процесса расходуется часть базового тока, обозначенная как J ЭП. Расчет этого тока даже в упрощенном варианте весьма сложен. Поэтому мы воспользуемся готовым решением, выполненным Са-Нойсом-Шокли для случая одного уровня ловушки:
, (66)
где 
,
,
.
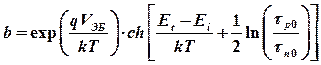Здесь Еt - энергия уровня ловушки, Еi - энергия середины запрещенной зоны, tp 0 и tn 0 - параметры модели рекомбинации Холла-Шокли-Рида, V 0 и W ЭП - контактная разность потенциалов и толщина слоя объемного заряда эмиттерного перехода соответственно.
Формула (66) скорее носит иллюстративный характер. Для расчетов чаще пользуются эмпирической зависимостью для тока рекомбинации в объемном заряде:
, (67)
где J ЭП0 и nV -эмпирические константы. Обычно значение коэффициента nV находится в диапазоне от единицы до двух (ближе к двум) и зависит от характера рекомбинационных центров. Чтобы определить, от каких параметров зависит J ЭП0, надо приравнять правые части уравнений (66) и (67). Получим:
J ЭП0 = 
. (68)
Если аргумент гиперболического синуса много больше единицы, что всегда реализуется в активном режиме работы транзистора, то
.
С учетом этого (68) примет вид
J ЭП0 = 
. (69)
Принимая во внимание, что толщина слоя объемного заряда перехода зависит от приложенного напряжения по закону
, (70)
где W 0 - равновесная толщина слоя объемного заряда эмиттерного перехода, выражение (69) может быть записано в виде
J ЭП0 =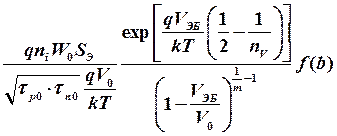 
. (71)
Здесь m - коэффициент, зависящий от профиля распределения примеси в переходе и может изменяться от двух (для резкого перехода) до трех (для плавного перехода). Поскольку левая часть уравнения (71) не зависит от напряжения на переходе, а в правую входит ряд сомножителей, зависящих от напряжения, то следует предположить, что комбинация этих последних сомножителей дает некоторую константу (обозначим ее Q). С учетом введенного обозначения формула (71) примет вид
J ЭП0 =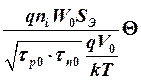 
. (72)
Подставляя (72) в (67), получаем для тока рекомбинации в слое объемного заряда эмиттерного перехода выражение
J ЭП =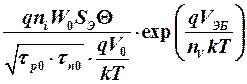 
. (73)
Таким образом, рекомбинационные потери в слое объемного заряда эмиттерного перехода, с учетом (13), можно записать в виде
R ЭП= 
. (74)
Обозначим 
, тогда для R ЭП получим:
R ЭП = 
. (75)
Существенное значение для рекомбинационных потерь в объемном заряде эмиттерного перехода имеют геометрические размеры. Чем меньше W 0 и W A, тем меньше данный параметр. Но в отличие от предыдущих составляющих рекомбинационных потерь R ЭП зависит также от напряжения на эмиттерном переходе. Поскольку nV больше единицы, то показатель экспоненты отрицателен. Это означает, что с ростом напряжения на переходе уменьшается рассматриваемая составляющая рекомбинационных потерь.
Можно формулу (75) переписать через ток коллектора (13):
. (76)
Видно, что с ростом тока коллектора 
уменьшается. Иначе говоря, можно повысить коэффициент передачи тока транзистора, заставляя его работать при повышенных плотностях коллекторного тока.
