Для строгого решения задачи о рекомбинационных потерях в пассивной базе необходимо решать двумерное уравнение непрерывности. Сложности, возникающие на этом пути, не окупают достигаемого результата. Поэтому с точностью, достаточной для инженерных расчетов, рассмотрим упрощенный вариант, представленный на рис. 9, на котором изображен фрагмент пассивной базы. Будем считать, что все носители заряда, инжектированные из эмиттера в пассивную базу, в ней же и рекомбинируют. При этом можно использовать одномерное приближение. Будем считать, что легирование базы в направлении оси y не меняется, а зависит только от х. Поскольку размеры пассивной базы в направлении у, как правило, существенно больше диффузионной длины неосновных носителей заряда, то можно считать, что с торца эмиттерного перехода дырки инжектируются в полубесконечную среду.
Рис.9. Одномерная модель тока JП
Тогда их распределение по координате у будет экспоненциальным:
, (46)
где LП - диффузионная длина неосновных носителей заряда в пассивной базе. Граничное значение дырок р (0) при у =0 определяется соотношением
р (0) = рn 0(х) 
, (47)
где рn 0 - равновесная концентрация дырок в базе, зависящая от координаты х. Все было бы просто, если бы концентрация примеси не зависела от х. Введем понятие средней концентрации примеси в пассивной базе и, соответственно, среднее значение инжектированных носителей:
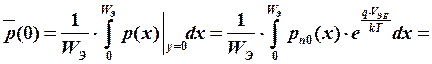
,(48)
где N П - концентрация типозадающей примеси в пассивной базе.
Зная распределение дырок по координате, нетрудно рассчитать, сколько их рекомбинирует в единицу времени во всей пассивной базе и таким образом определить ток J П.
Учитывая, что скорость рекомбинации неравновесных носителей заряда определяется соотношением
, (49)
где 
- среднее значение времени жизни в пассивной базе, общее количество дырок, рекомбинирующих во всей пассивной базе, будет равно:
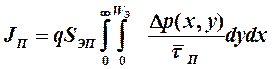, (50)
где S ЭП - площадь эмиттерного перехода, граничащая с пассивной базой. Учитывая, что равновесная концентрация неосновных носителей заряда в пассивной базе крайне мала, ею можно пренебречь и считать, что D р (x,y) = pn (x,y). Распределение же концентрации неосновных носителей pn (x,y) с учетом (46), (47) и (48) можно свести к функции одной переменной:
. (51)
Тогда составляющая тока базы, обеспечивающая рекомбинацию в пассивной базе с учетом (51) и (50), будет равна:
. (52)
Теперь, используя выражение для тока коллектора (13), легко определить рекомбинационные потери в пассивной базе:
(53)
Рассмотрим, какие факторы влияют на величину этих потерь. Во-первых, влияет соотношение площадей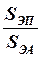 
; во-вторых, - соотношение концентраций 
; в-третьих, - толщина активной базы WA; в четвертых, - диффузионная длина неосновных носителей заряда в пассивной базе tП.
Очевидно, что для повышения коэффициента передачи тока транзистора необходимо воздействовать на перечисленные факторы в сторону снижения рекомбинационных потерь в пассивной базе. Чтобы уменьшить отношение 
= 
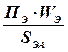(где ПЭ - периметр эмиттера, W Э - глубина залегания эмиттерного перехода), надо уменьшать отношение периметра к площади эмиттера и уменьшать глубину залегания эмиттерного перехода. Известно, что наименьшее отношение периметра к площади имеет круг. Поэтому, с точки зрения минимизации рекомбинационных потерь в пассивной базе, круглая форма эмиттера предпочтительнее квадратной и тем более – прямоугольной. Хотя с экономической точки зрения это далеко не лучший вариант, т.к. приводит к повышению стоимости транзистора.
Если же эмиттер выполнен в виде круга, то его периметр ПЭ = 2p r Э, а площадь - SЭА = 
. Тогда отношение периметра к площади будет равно 
. А отношение площадей: 
. Таким образом, чем больше линейные размеры эмиттера, тем меньше рекомбинационные потери в пассивной базе.
Следует также отметить, что уменьшение толщины активной базы также способствует уменьшению рекомбинационных потерь в пассивной базе.
Поскольку средняя концентрация примеси в пассивной базе существенно больше, чем в активной, то можно полагать, что высокий уровень инжекции в ней для реальных уровней тока коллектора не наступает. Следовательно, при высоком уровне инжекции в активной базе потери в пассивной базе с учетом (18) оказываются пропорциональны току коллектора:
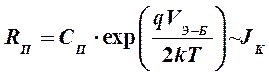, (54)
где СП - коэффициент пропорциональности.
