Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. e, резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток
I 0 = ei / R
(внутренним сопротивлением источника тока пренебрегаем).
В момент времени t= 0 отключим источник тока. Ток через катушку индуктивности L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции eS 
, препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I = eS / R, или
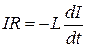. (17.5)
Разделив в выражении (17.5) переменные, получим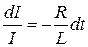 
. Интегрируя это уравнение по I (от I 0 до I) и t (от 0 до t), находим 
, или
, (17.6)
где 
— постоянная, называемая временем релаксации. Из (17.6) следует, что t есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (17.6) и определяется кривой 1 на рис. 17.1. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше t и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При замыкании цепи помимо внешней э.д.с. e возникает э.д.с. самоиндукции eS , препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома, IR = e + eS, или
IR = e 
.
Введя новую переменную 
e, преобразуем это уравнение к виду
,
где t — время релаксации.
В момент замыкания (t =0) сила тока I = 0 и U = e. Следовательно, интегрируя по U (от - e до IR- e) и t (от 0 до t), находим 
, или
, (17.7)
где 
e / R установившийся ток (при t ® 0).
Рис. 17.1.
Таким образом, в процессе включения источника э.д.с. нарастание силы тока в цепи задается функцией и определяется кривой 2 на рис.17.1. Сила тока возрастает от начального значения I = 0 и асимптотически стремится к установившемуся значению e / R. Скорость нарастания тока определяется тем же временем релаксации 
, что и убывающие тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.
Оценим значение э.д.с. самоиндукции eS, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R 0 до R. Предложим, что мы размыкаем контур, когда в нем течет установившийся ток 
. При размыкании цепи ток изменяется по формуле (17.6). подставив в нее выражение для I 0 и t, получим
.
Э.д.с. самоиндукции
eS 
e 
,
т.е. при значительном увеличении сопротивления цепи 
обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, т.к. это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
