Зависимость изменения вторичного напряжения трансформатора от коэффициента нагрузки

Согласно ГОСТ, изменением напряжения трансформа­тора при заданном коэффициенте мощности называют алгебраическую разницу между номинальным вторичным напряжением и напряжением, устанавливающимся на за­жимах вторичной обмотки при номинальных значениях вторичного тока, частоты и первичного напряжения,

Пример 1. Определить ΔU трансформатора в процен­тах, если U_2H = 400 в, U₂ = 380 в.

Решение:

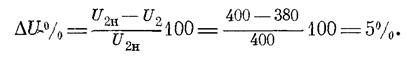
ΔU трансформатора можно определять путем снятия его внешней характеристики.

Внешней характеристикой трансформатора называют зависимость напряжения на зажимах вторичной обмотки от тока нагрузки при постоянном первичном напряже­нии, частоте и cos φ₂.

Как видно из рисунка 98, на котором представлены внешние характеристики трансформатора при cos φ ₂ = 1 — активная нагрузка (кривая 1) и при cos φ ₂ = 0,8 — актив­но-индуктивная нагрузка (кривая 2), напряжение транс­форматора с увеличением нагрузки уменьшается, причем при активно-индуктивной нагрузке изменение напряже­ния будет большее, чем при активной.

ΔU можно определить по внешней характеристике, если высчитать разницу между U_{2 Н} при холостом ходе и U₂ при номинальной нагрузке.

Этот способ определения ΔU не применяют, так как он неэкономичен, потому что для снятия внешней харак­теристики нужно нагрузить трансформатор на полную мощность, кроме того, этот способ недостаточно точен, так как нужно измерять боль­шие напряжения.

ΔU определяют аналитиче­ски. Выведем формулу для опре­деления ΔU при помощи упро­щенной векторной диаграммы трансформатора.

Рис 98 Внешние характеристики трансформатора

На рисунке 99, а изображена упрощенная векторная диаграм­ма трансформатора при холо­стом ходе. Векторная диаграмма представлена одним вектором ОA U₁ =U'₂ так как при холостом ходе, если мы током холостого хода пренебрегаем, I ₁ = I₂ = 0, а у приведен­ного трансформатора

Векторная диаграмма при нагрузке представлена на рисунке 99, б. Здесь U'₂ меньше U₁ вследствие того, что в обмотках трансформа­тора есть падение напряжения I₁z_K Алгебраическая разность между величиной U₁ и U₂ и дает вели­чину ΔU.

Построим упрощен­ную векторную диаграм­му нагруженного транс­форматора, пристроив к концу вектора напря­жения U'₂ треугольник короткого замыкания ABC, катеты которого обозначим U_а = I₁r_к и U_p = I₁x_к, а гипотенузу через U_к = I₁z_к. Сделав засечку радиусом U'₂ на вектор U₁, получим алгебраическую раз­ницу между векторами U₁ — U'₂ = ΔU

(рис. 100). Про­должим вектор U₂ до величины, равной U₁ , и затем

Рис 99 Упрощенная векторная диаграмма трансформатора

a — при холостом ходе, б — при нагрузке

проведем дугу радиусом U ₁ до пересечения ее с продол­жением линии вектора U'₂. Отрезок AD = КС = AU.

Из точки С проведем линию, перпендикулярную к ли­нии OD, до пересечения с нею в точке М. Из вершины прямого угла треугольника короткого замыкания про­ведем линию BF, перпендикулярную к линии OD, до пересечения с нею в точке F.

Тогда ΔU = AF + + FM+MD. Но отрезок MD —величина очень малая по сравнению с отрезками AF и FM, поэтому им можно пре­небречь и определять ΔU как сумму отрезков AF и FM, т. е. ΔU = AF + FM.

Проведем из точки В линию BL, параллель­ную линии OD, до пе­ресечения ее с продол­жением линии СМ в точке L. В получив­шемся прямоугольнике сторона BL = FM.

Рассмотрим треу­гольник CBL и треуголь­ник AFB. В треуголь­нике CLB угол LCB равен ф₂ вследствие того, что CL _┴ OD, a С В _┴ I ₁; а в треуголь­нике FAB угол FAB также равен φ₂, так как линия OD пересекает две парал­лельные линии АВ и I ₁. Тогда

Часто значения U_a и U_р даются в процентах, тогда

где k_нг — коэффициент нагрузки трансформатора;

Uа% и U_р% можно определить, если известны S_H, Р_к и U_к трансформатора.

U_a% — это отношение падения напряжения на актив­ном сопротивлении обмоток к номинальному напряжению, т. е.

Умножим числитель и знаменатель дроби на I_1н

Но так как Р_к берется в ваттах (вт), а S_H в киловольт-амперах (ква), то умножаем знаменатель на 1000

где Р_к дано в ваттах, a S_н — в киловольтамперах. Зная U_k% и U_а%, можно найти U_р%

Величина ΔU% для советских трансформаторов при значениях cos φ₂ = 0,8 и U_K = 5,5 ÷10,5% находится в пределах 4—8% U_н.

На рисунке 101 при­ведены кривые зависи­мости изменения напря­жения трансформатора мощностью 100 ква, U = 6300/220 в от коэф­фициента нагрузки при различных значениях cosφ₂.

Вверх от оси абсцисс отложены зна­чения ΔU при активной и активно-индуктивной нагрузке, а вниз от оси абсцисс при актив­но-емкостной нагрузке. При активно-емкостной нагрузке напряжение на зажимах трансформа­тора при увеличении нагрузки повышается (см. рис. 94).

Пример 2. Определить ΔU% для трансформатора мощностью S_н = 100 ква, при cos φ₂ = 0,8, если U_к = 5,5%, Р_к = 2400 вт.

Решение. Находим U_a%:

Находим U_р%:

БИЛЕТ 23