Активно-емкостная нагрузка трансформатора

Как известно, при холостом ходе трансформатора в первичной обмотке протекает ток I ₀, который создает м. д. с. I₀ ω₁, а эта м.д.с. создает основной магнитный поток Ф и поток рассеяния Ф_рс1. Основной магнитный поток Ф индуктирует в обмотках трансформатора э. д. с. Е₁ и Е₂ . Если к зажимам вторичной обмотки трансфор­матора ах подсоединить нагрузку с сопротивлением z_нг, то по вторичной обмотке потечет ток I₂, отстающий от э.д. с. Е₂ на угол ψ(рис. 92, а).

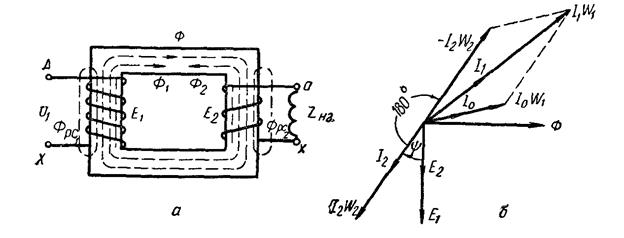
Рис 92 Работа трансформатора при нагрузке:

а — принципиальная схема нагруженного трансформатора,

б — векторная диаграмма м.д.с. трансформатора

 

Умножив ток I ₂ на число витков вторичной обмотки ω₂, получим вектор м. д. с. вторичной обмотки I₂ ω₂, который отложим по направлению вектора тока I₂, так же как м. д. с. при холостом ходе I₀ ω₁ (рис. 92, б).

При появлении тока нагрузки во вторичной обмотке соответственно увеличивается ток в первичной обмотке, где вместо тока I ₀ протекает ток I₁ создающий м. д. с. I₁ ω₁. По формуле (77) э. д. с. первичной обмотки Е₁ = = 4,44 f₁ ω ₁ Ф_м . Пренебрегая падением напряжения в пер­вичной обмотке, предположим, что

Если напряжение и частота в сети постоянны по величине, то можно написать следующее равенство:

Но в формуле 4,44, f₁ и ω₁— постоянные числа, сле­довательно при постоянном напряжении и частоте в сети магнитный поток трансформатора будет величиной по­стоянной и от нагрузки зависеть не будет, т. е.

Это уравнение называют уравнением м. д. с. трансфор­матора. М. д. с. трансформатора при холостом ходе I₀ ω₁ и во вторичной обмотке I₂ ω₂ нанесены на диаграмму.

Из уравнения м. д. с. определим м. д. с. первичной об­мотки, она равна:

(82)

т. е. для получения м. д. с. первичной обмотки I₁ ω₁нужно к м. д. с. холостого хода I₀ ω₁прибавить м. д. с. вто­ричной обмотки I₂ ω₂с обратным знаком, т. е. повернув вектор этой м. д. с. на 180°.

Сложив векторы этих м. д. с, получим м. д. с. первичной обмотки I₁ ω₁(рис. 92, б). Как видно из векторной диаграммы, м. д. с. первичной обмотки намагничивает сердечник трансформатора, а м. д. с. вторичной обмотки его размагничивает. Геометрическая сумма векторов м. д. с. первичной и вторичной обмоток дает вектор результирующей м. д. с, которая равна м. д. с. трансформатора при холостом ходе I₀ ω₁и создает магнитный поток Ф.

Можно рассматривать вопрос и так, что м. д. с. пер­вичной обмотки создает магнитный поток Ф₁, намагни­чивающий трансформатор, а м. д. с. вторичной обмотки магнитный поток Ф₂, размагничивающий его, в резуль­тате в сердечнике образуется магнитный поток Ф.

Ток в первичной обмотке I₁ создает также магнитный поток рассеяния Ф_РС1, силовые линии которого не сцеп­ляются с вторичной обмоткой, а замыкаются по воздуху, а ток вторичной обмотки I₂ создает аналогично магнитный поток рассеяния Ф_рс2.

Разделим обе части уравнения м. д. с. трансформатора на ω₁:

Величину называют приведенным током.

Рассмотрим, что такое приведенная величина и какова цель приведения.

Так как числа витков первичной и вторичной обмоток трансформатора разные, то э. д. с. и токи в этих обмотках также неодинаковы. Они отличаются в k или в 1/k раз.

Поэтому сопоставлять эти величины или строить вектор­ные диаграммы, где величины вторичной и первичной обмоток нужно складывать, нельзя, как нельзя сложить расстояния, измеренные на картах разных масштабов, не приведя их к одному масштабу.

Например, нельзя было бы получить величину паде­ния напряжения в нагруженном трансформаторе путем непосредственного суммирования падений напряжения каждой из обмоток. Так как эти обмотки имеют разные по величине токи и сопротивления, то и векторы, выра­жающие величину падений напряжения, неодинаковы по величине для каждой обмотки.

В трансформаторах величины вторичной обмотки при­водят к первичной так же, как расстояния, измеренные на картах разных масштабов, приводят к одному масштабу, т. е. обычный трансформатор заменяют приведенным, у ко­торого число витков первичной обмотки ω₁равно числу витков вторичной обмотки ω₂или k= 1. Приведенные величины обозначают штрихом вверху. Для приведения э. д. с. ее нужно умножить на коэф­фициент трансформации, так как во вторичной обмотке она меньше в kраз

(83)

Аналогично приводится напряжение и другие э. д. с. в трансформаторе.

При приведении тока соблюдают условие, чтобы кажу­щаяся мощность вторичной обмотки после приведения не изменилась, т. е. Е₂I₂ = Е₂’ ^.I₂’ Отсюда

(84)

т. е. для приведения тока его нужно разделить на коэф­фициент трансформации.

При приведении активного сопротивления исходят из условия, чтобы потери в меди приведенного трансфор­матора не изменились

откуда

(85)

т. е. для приведения активного сопротивления его нужно умножить на квадрат коэффициента трансформации.

Так как E_рс2 = I₂x₂, то

(86)

т. е. аналогично с активным сопротивлением.

(87)

значит, для приведения любого сопротивления его нужно умножить на квадрат коэффициента трансформации.

Построим векторную диаграмму трансформатора при активно-емкостной нагрузке. В этом случае ток опережает э. д. с. на угол ψ₂. Построение ведем как и для векторной диаграммы при активно-индуктивной нагрузке.

Рис. 94. Векторная диаграмма трансформатора при активно-емкостной нагрузке:

а — полная, б — для вторичной обмотки.

Как видно из диаграммы (рис. 94), в этом случае с уве­личением нагрузки напряжение на зажимах вторичной обмотки трансформатора возрастает.

Для рассмотрения процессов, происходящих в транс­форматорах, пользуются схемой замещения. В схеме замещения каждая обмотка трансформатора заме­щена реальными активным и индуктивным сопротивле­ниями, которыми она обладает, и идеальной обмоткой без сопротивления. Кроме этого, принимаем, что дей­ствие э. д. с. рассеяния эквивалентно падениям напря­жения на индуктивных сопротивлениях обмоток транс­форматора, а действие э. д. с. активных сопротивлений — падениям напряжения на активных сопротивлениях об­моток.

Таким образом, первичная обмотка состоит из реаль­ных сопротивлений х₁ и r ₁ и идеальной обмотки z_1M, а вто­ричная соответственно из х'₂, r'₂ и Z'_2M (рис. 95, а). Обмотки z_1m и Z'_2m связаны между собой электромагнитно посред­ством магнитного потока Ф_м, создающего в обмотках транс­форматора э. д. с. Е₁ и Е'₂.

Так как мы рассматриваем приведенный трансформа­тор, у которого ω₂ = ω₁ а k = 1, то можно электромаг­нитную связь заменить электрической, объединив об­мотки z_lM и z’_2m в одну z₁₂, по которой течет ток,

Обмотку z₁₂ называют намагничивающей обмоткой, или намагничивающей ветвью, в которой создается магнитный поток Ф_м током I ₀ (рис. 95, б). Напряжение на зажимах намагничивающей обмотки равно Е₁ = Е'₂.

Данная схема замещения соответствует полной век­торной диаграмме трансформатора (рис. 93).

Схему замещения трансформатора и соответственно векторную диаграмму можно упростить. С этой целью пре­небрегают намагничивающим током I₀, так как он не пре­вышает в среднем 5% I _Н для большинства трансформа­торов, и намагничивающей ветвью схемы замещения z₁₂.

Тогда упрощенная схема замещения будет состоять из последовательно соединенных сопротивлений г₁, х₁ и r'₂, х₂, по которым протекает ток I₁, так как в приведен­ном трансформаторе ток I₁ = I₂, если пренебречь током холостого хода.

К зажимам АХ в схеме замещения подведено напря­жение U₁, а на зажимах ах мы получаем напряжение U'₂, которое меньше U₁, на величину изменения напряжения

Рис. 95. Схема замещения трансформатора при нагрузке:

а — схема трансформатора, б — схема замещения трансформатора;

в — упрощенная схема замещения, г — упрощенная векторная

диаграмма

вследствие падения напряжения в обмотках трансфор­матора от тока нагрузки I ₁ (рис. 95, в).

Соответствующую этой схеме замещения упрощенную векторную диаграмму трансформатора строим, исходя из тех же соображений — вектором тока холостого хода пренебрегаем, а все вторичные векторы поворачиваем на 180°. Вектор тока I ₁ = I'₂ проводим вертикально, затем под углом φ₂ откладываем вектор напряжения U'₂ (рис. 95, г). С вектором тока совпадает по фазе падение напряжения на активном сопротивлении вторичной об­мотки I'₂r '₂, а перпендикулярно к вектору тока — падение напряжения на индуктивном сопротивлении вторичной обмотки I'₂ x'₂- Замыкающий вектор ОА — это вектор э. д. с. Е₁ = Е'₂.

Рис. 96. Упрощенная схема замещения трансформатора при нагрузке:

a — схема замещения; б — упрощенная векторная диаграмма.

С конца вектора э. д. с. откладываем вектор падения напряжения на активном сопротивлении первичной об­мотки I₁r ₁, а перпендикулярно к вектору тока — на индук­тивном I₁x ₁. Вектор ОВ — напряжение сети U₁.

Падения напряжения на активных сопротивлениях обеих обмоток можно объединить, то же можно сделать и по отношению падений напряжения на индуктивных сопротивлениях обеих обмоток

 

 

Сопротивления

а также z_K называют активным, индуктивным и пол­ным сопротивлениями короткого замыкания трансфор­матора, или параметрами короткого замыкания трансфор­матора.

Тогда схема замещения трансформатора упрощается еще больше. Она будет состоять из двух сопротивлений r_к и х_к, по которым протекает ток I ₁ (рис. 96, а).

Соответствующая этой схеме замещения векторная диаграмма приведена на рисунке 96, б. Обычно

БИЛЕТ 22