При исследовании динамических моделей эк-ки часто оказывается необходимо не только уметь численно решать возникающие в ходе моделирования уравнения, но и получить некоторое общее описание структуры множества всех возможных траекторий динамической системы. Важную роль при таком описании играют траектории, имеющие максимально простую структуру.
Определение: Последовательность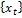 
, являющаяся решением разностного уравнения 
(1), называется стационарной траекторией динамической системы (1), если она представляет собой последовательность: 
, 
.
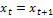Из определения непосредственно вытекает метод отыскания стационарных траекторий системы (1): достаточно найти корни следующего уравнения: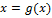 
(2), где 
.
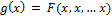Определение: Всякое решение 
ур-ния (2) называют стационарным состоянием, или состоянием динамического равновесия системы (1).
Последовательности вида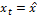 
, и только они, являются стационарными траекториями этой системы.
Следующая теорема поясняет роль стационарных траекторий при исследовании динамических систем в дискретном времени.
Теорема. Пусть последовательность 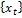является траекторией динамической системы (1) и при этом имеет предел 
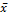. Тогда 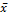есть стационарное состояние системы (1).
Доказательство: Переход к пределу в обеих частях уравнения (1) с учетом предположения о непрерывности ф-ии F приводит к равенству: 
. Т.о., 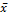есть стационарное состояние системы (1). Теорема доказана.
Теперь введем одно из важнейших с точки зрения моделирования эк.динамики понятий – понятие об устойчивости динамического равновесия. Ограничимся при этом частным случаем системы (1), когда порядок разностного уравнения – первый, т.е. когда это уравнение имеет вид: 
(3).
Пусть динамическая система, описываемая разностным уравнением (3) обладает стационарным состоянием .
Определение: Стационарное состояние называется локально устойчивым, если существует такая ε-окрестность точки , что все траектории, начальные состояния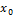 
которых принадлежат этой окрестности, сходятся к .
Смысл локальной устойчивости состоит в том, что если система изначально не слишком удалена от стационарной траектории, то есть если величина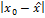 
не слишком велика, то с течением времени система оказывается все ближе (в асимптотике сколько угодно близко) к стационарной траектории.
Существует также другой, более сильный тип устойчивости.
Определение: Стационар. состояние называется глобально устойчивым, если все траектории уравнения (3) сходятся к .
Ясно, что глобально устойчивое динамическое равновесие одновременно является локально устойчивым. Обратное утверждение, вообще говоря, неверно. Однако оно верно для достаточно узкого, но важного класса разностных уравнений – линейных разностных уравнений с постоянными коэффициентами.
