Чтобы выяснить взаимное положение дуги и отрезка прямой, следует (рис.124):
- из центра дуги опустить перпендикуляр на прямую;
- определить точку(XP,YP) пересечения перпендикуляра с прямой;
- измерить текущий угол перпендикуляра U;
- повернуть прямую вокруг
центра дуги на угол (-U);
Координата Х точки А будет
Рис. 124 равна расстоянию от центра дуги до прямой, а координата Y будет найдена как катет прямоугольного треугольника при известных гипотенузе, равной радиусу дуги, и другому катету.
- вернуть точки в исходное положение.
Программное описание оператора:
begin
TekUgol(X1,Y1,X2,Y2,U0);
DwaOtr(X1,Y1,U0,X,Y,90+U0,XP,YP,P);
DlinaO(XС,YС,XР,YР,L);
DlinaO(XС,YС,XN,YN,R);
if L > R then P:=0; {не пересекаются}
else if (L - R) < 0.05 then begin
P:=1; XA:=R; XB:=R; YA:=0; YB:=0;
{прямая касается дуги в точке(XP,YP)}
end
else begin
TekUgol(XC,YC,XP,YP,U);
XA = L; XB= -L; {координаты Х точек А и В после
поворота на угол (- U)}
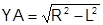;YB = - YA; {координаты Y точек
А и В после поворота на угол (- U)}
end;
XTS:=XT; YTS:=YT; UgS:=Ugol;
Ugol:=U; XT:=XC; YT:=YC;
PX[1]:=XA; PY[1]:=YA; PX[2]:=XB; PY[2]:=YB;
Preobr(2);
XA:=PX[1]; YA:=PY[1]; XB:=PX[2]; YB:=PY[2];
{координаты точек А и В после возврата в
исходное положение}
XT:=XTS; YT:=YTS; Ugol:=UgS; {координаты точек пересечения возвращены в исходную систему координат чертежа}
end;
Оператор: OtrDug(X1,Y1,Ug,XC,YC,R,XP1,YP1,XP2,YP2,P).
Остается выяснить принадлежность точек А и В исходным отрезку прямой и дуге, используя известные операторы:
PikOtr(XA,YA,X1,Y1,X2,Y2,P) ® P=1
PikOtr(XB,YB,X1,Y1,X2,Y2,P) ® P=0
PikDug(XA,YA,XC,YC,XN,YN, XK,YK,напр.,P)® P=1
PikDug(XB,YB,XC,YC,XN,YN, XK,YK,напр.,P)® P=1.
Отсюда следует, что точка А является точкой пересечения отрезка и дуги, точка В - нет, т.к. она не принадлежит отрезку (Р=0).
Пересечение дуг
Для определения точек А и В пересечения двух окружностей с центрами (XC1,YC1), (XC2,YC2) и радиусами R1, R2 следует (рис. 125):
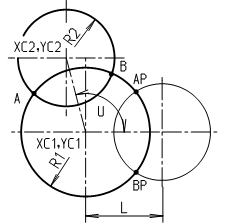- определить расстояние L между центрами окружностей;
- определить текущий угол U прямой, соединяющей центры;
- повернуть вторую окружность вокруг центра первой окружности на угол (- U);
После поворота координаты точек пересечения определяются системой уравнений
.
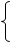
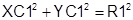
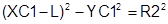- вернуть точки пересечения
окружностей в исходное положение.
Рис. 125
Программное описание оператора:
begin
DlinaO(XС1,YС1,XC2,YC2,L);
TekUgol(XC1,YC1,XC2,YC2,U);
if (R1+R2<L) or (L+R1<R2) or (L+R2<R1) or (L<0,001) then
begin
P:=0; {нет пересечения}
end
else begin
; 
;
; 
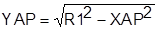; {решена система уравнений
при условии, что угол U = 0}
XTS:=XT; YTS:=YT; UgS:=Ugol;
Ugol:= U; XT:=XC1; YT:=YC1; {введены угол возврата
точек пересечения и текущая база}
PX[1]:=XAP; PY[1]:=YAP; PX[2]:=XBP; PY[2]:=YBP;
{заполнен массив точек}
Preobr(2); {выполнен возврат точек в исходное положение}
XA:=PX[1]; YA:=PY[1]; XB:=PX[2]; YB:=PY[2]; {выполне-
ны присвоения значений координат точек А и В}
XT:=XTS; YT:=YTS; Ugol:=UgS; {координаты точек пересечения возвращены в исходную систему координат чертежа}
end;
end;
Оператор: DugDug(XC1,YC1,R1,XC2,YC2,R2,X1,Y1,X2.Y2,P).
Остается определить принадлежность точек дугам:
PikDug(XA,YA,XC1,YC1,XN1,YN1, XK1,YK1,напр.,P)® P=1
PikDug(XB,YB,XC1,YC1,XN1,YN1, XK1,YK1,напр.,P)® P=1.
PikDug(XA,YA,XC2,YC2,XN2,YN2, XK2,YK2,напр.,P)® P=1
PikDug(XB,YB,XC2,YC2,XN2,YN2, XK2,YK2,напр.,P)® P=1.
Направление дуги
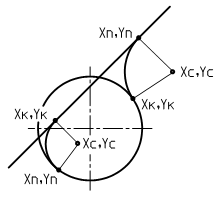
Оператор предназначен для автоматического распознавания направления выполняемой дуги по начальной и конечной точкам и центру (рис. 126).
Procedure Naprawl(Xc,Yc,Xn,Yn,Xk,Yk: Float;напр.: byte);
var U1,U2,UU: Float;
begin
TekUgol(Xc,Yc,Xn,Yn,U1);
TekUgol(Xc,Yc,Xk,Yk,U2);
{текущие углы начальной
и конечной точек дуги}
UU:=abs(U1-U2);
if (U1<U2) and (UU<180)
then напр:=1
else if (U1<U2) and (UU>180)
then напр:=2
else if (U1>U2) and (UU<180)
then напр:=2
else напр:=1;
Рис. 126 end;
Оператор: Naprawl(Xc,Yc,Xn,Yn,Xk,Yk,напр);
Взаимное положение линий
Procedure
Tch_NiK(X Cg,YCg,Xg1,Yg1,Xg2,Yg2,Xs,Y s,X Tn,YTn,LD k);
¯
параметры ввода вывода
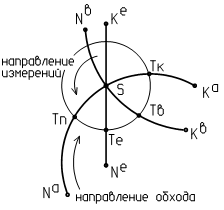
Дуга NOKO в точке S пересекается с прямой NеKе и дугой NвKв (рис. 127). Направление обхода принимают совпадающим с направлением от начальной точки к конечной начального элемента NOKO. По отношению к начальному элементу определяется положение текущих элементов NеKе и NвKв.
Цель – определить траекторию движения по контуру NOS - SNе –
Рис. 127 NеS - SKв - KвS - SKO и т.д. в бесконечном цикле если не будет назначен конечный элемент. Одновременно можно определить, что элементы SNе и SKв расположены внутри дуги NOKO.
С центром в точке пересечения S начального элемента с текущим выполнена дуга измерения радиусом LS (текущая точность измерения). Если рассматривается внутренняя область, то направление измерений (ход) противоположно направлению обхода. Ближайшая к NO точка Tn – начальная, Tk – конечная.
Максимальная длина дуги LDk от Tn до Тk. Если длины дуг от Tn до Te и от Tn до Tb меньше максимальной, то точки Те и Tb расположены внутри дуги NOKO, равно как и отрезки SNe, Skb. Если двигаться по дуге NOKO в направлении ‘обхода’, то первым встретим отрезок SNe, затем - дугу SKb. Те же отрезки прямой и дуги находятся внутри области, ограниченной дугой NOKO.
begin
if Obhod=1 then Hod:=2 else Hod:=1; {определено направление
измерений ‘Hod’ для внутренней области}
Элемент, по отношению к которому определяется положение других линий, отрезок прямой:
if El=1 then begin
Определим точки пересечения отрезка прямой и окружности:
TekUgol(Xg1, Yg1, Xg2, Yg2,Ug);
OtrDug(Xg1,Yg1,Ug,Xs,Ys,Ri,XP1,YP1,XP2,YP2,P);
{Ri - радиус окружности измерения дуги}
Найдем точки начала(XTn,YTn) и конца(XTk,YTk) измерений:
DlinaL(Xg1,Yg1,XP1,YP1,L1);
DlinaL(Xg1,Yg1,XP2,YP2,L2);
if L1<L2 then begin
XTn:=XP1; YTn:=YP1; XTk:=XP2; YTk:=YP2;
end
else begin
XTn:=XP2; YTn:=YP2; XTk:=XP1; YTk:=YP1;
end;
Выясним принадлежность точки Tk отрезку прямой:
PikOtr(XTk,YTk,Xg1,Yg1,Xg2,Yg2,P);
Определим LDk:
if P=1 then LDk:=180 else LDk:=360;
{Ldk - max угол, при LD<=LDk точка находится внутри области.
Если S совпадает с концом отрезка прямой, LDk=360. В другом
случае LDk=180}
end
Элемент, по отношению к которому определяется положение других линий, дуга:
else begin
Определим точки пересечения дуги и окружности:
DugDug(XCg,YCg,R,Xs,Ys,Ri,XP1,YP1,XP2,YP2,P);
Определим длины дуг от начальной точки дуги (Xg1,Yg1) до точек пересечения (XP1,YP1), (XP2,YP2):
DlinaD(XСg,YCg,Xg1,Yg1,XP1,YP1,Nag,LD1);
DlinaD(XCg,YCg,Xg1,Yg1,XP2,YP2,Nag,LD2);
Найдем точки начала(XTn,YTn) и конца(XTk,YTk) измерений:
if LD1<LD2 then begin
XTn:=XP1; YTn:=YP1; XTk:=XP2; YTk:=YP2;
end
else begin
XTn:=XP2; YTn:=YP2; XTk:=XP1; YTk:=YP1;
end;
Определим LDk:
DlinaD(Xs,Ys,XTn,YTn,XTk,YTk,Hod,LDk);
end;
end;
3.3.11.Операторы работы с файлами
- открыть временный файл, записать строку параметров линии и
прорисовать ее:
RisLineBox(Bx, El, Napr, X1, Y1, X2, Y2, XC, YC), где:
Bx - номер временного файла или имя файла в зависимости от типа
переменной Bx;
El - определитель типа линии (1 - прямая, 2 - дуга);
Napr - направление дуги (1- против часовой стрелки, 2 - по часовой);
X1, Y1 - координаты начальной точки;
X2, Y2 - координаты конечной точки;
XC, YС - координаты центра дуги;
- прочитать файл линий, начиная с 1-й строки по Nк(последняя строка)
и заполнить строку переменных:
