На рисунке 2 представлена электрическая схема лабораторной установки, а на рисунке 3 – ее общий вид. В лабораторный стенд входят моделирующая и измерительная части.
Моделирующая часть включает в себя:
1. Источник переменного напряжения.
2. Понижающий трансформатор.
3. Гибкий токопровод с зажимами на концах.
4. Проводник, изготовленный из медной шины, расположенный в ферромагнитном пазу, площадь поперечного сечения проводника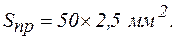 
5. Токоограничивающее сопротивление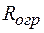 
(нагревательный элемент, изготовленный из нихрома).
6. Модель паза электрической машины. Модель паза состоит из штампованных и изолированных друг от друга листов электротехнической стали, стянутых болтами в пакет. Высота паза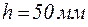 
, ширина паза 
.
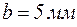Измерительная часть представлена аппаратно-программным измерительным комплексом (АПИК), в который входят:
1. Аналого-цифровой преобразователь (USB),
2. Персональный компьютер.
3. Гнезда для подключения входов USB- осциллографа.
4. Цифровой миллитесламетр, измеряющий магнитную индукцию по высоте проводника, расположенного в ферромагнитном пазу.
5. Датчик Холла, выходное напряжение которого пропорционально магнитной индукции, пронизывающей полупроводниковую пластину датчика Холла.
6. Трансформатора тока (ТТ).
7. Образцовое измерительное сопротивление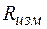 
(датчик тока).
8. Цифровой мультиметр.
9. Выключатель для сети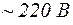 
.
Измерительная часть
При изучении поверхностного эффекта в ферромагнитном пазу измерение плотности тока в сечении проводника выполнить невозможно, поэтому используются косвенные измерения. Один из предпочтительных способов косвенного определения плотности тока в сечении проводника основывается на измерении магнитной индукции в ферромагнитном пазу.
Если для измерения магнитной индукции используется измерительная рамка с известной площадью сечения и числом витков, то распределение плотности тока по высоте проводника можно получить только через процедуру интегрирования напряжения, пропорционального наведенной в рамке ЭДС, используя аналоговый или цифровой интегратор. При этом цифровой метод интегрирования напряжения на выводах измерительной рамки с помощью USB – осциллографа, имеющем встроенный аналого-цифровой преобразователь (АЦП), и виртуального интегратора, построенного в среде LabView, является более предпочтительным, так как сопровождается большей точностью измерений.
Если для измерения магнитной индукции в ферромагнитном пазу используется цифровой мультиметр, измеряющий магнитную индукцию с помощью датчика Холла, то точность проводимых измерений по сравнению с известными методами оказывается существенно выше [2,3]. Воспользуемся преимуществами данного метода при изучении поверхностного эффекта в ферромагнитном пазу.
Методика определения плотности тока в сечении проводника, расположенном в ферромагнитном пазу сводится к следующему.
С помощью измерительного комплекса АПИК следует одновременно записать кривую напряжения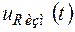 
на измерительном сопротивлении 
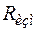, пропорциональном току 
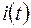в проводнике, и кривую выходного напряжения, снимаемого с датчика Холла, пропорционального магнитной индукции 
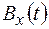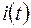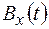при фиксированных значениях погружений датчика Холла в ферромагнитный паз. Затем по этим кривым необходимо определить сдвиг по фазе между и . По кривой 
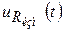, используя закон Ома, и значение коэффициента трансформации ТТ определяется кривая тока 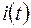в проводнике. По кривой выходного напряжения с датчика Холла с помощью коэффициента пересчета находятся значения магнитной индукции 
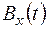по высоте проводника, расположенного в пазу.
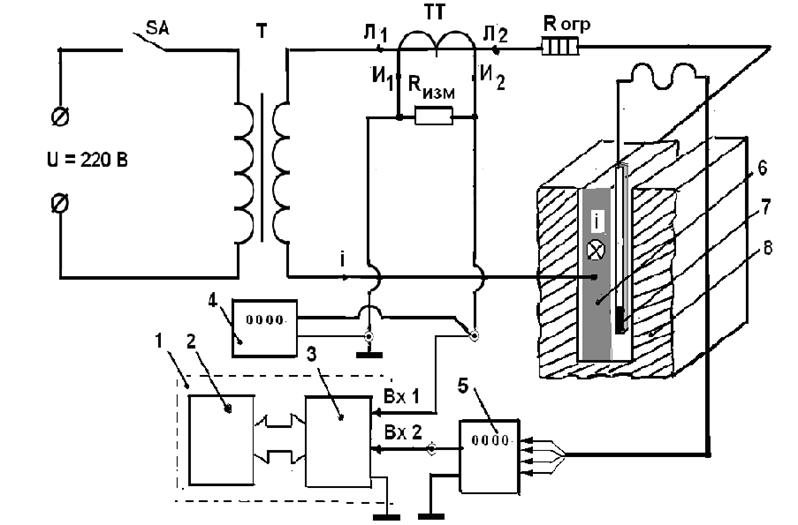
Рис. 2. Электрическая схема лабораторной установки по исследованию
поверхностного эффекта в ферромагнитном пазу: 1 – АПИК, 2 – компьютер,
3 – USB-осциллограф, 4 – цифровой вольтметр, 5- цифровой миллитесламетр,
6 – медная шина с током, 7 – датчик Холла, 8 – ферромагнитный паз.
Измеренные с помощью АПИК мгновенные значения магнитной индукции, хранящиеся в протоколе испытаний в памяти компьютера, позволяют определить распределение плотности тока по высоте проводника, используя численную процедуру вычисления производной
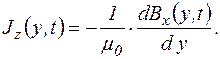(34)
При упрощенном анализе поверхностного эффекта в ферромагнитном пазу процедура взятия производной в формуле (34) заменяется вычислением конечных разностей, и тогда
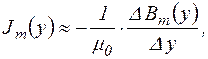(35)
где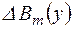 
– разность амплитудных значений магнитной индукции в точках, отстоящих друг от друга на расстоянии 
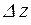по высоте проводника, 
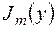- амплитудное значение плотности тока в сечении проводника.
