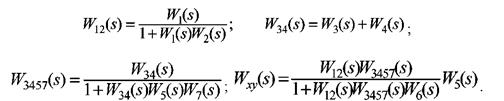Користуючись отриманими правилами структурних перетворень, довільні структурні схеми реальних замкнутих САК можна перетворити до одноконтурного вигляду, наведеного на рис. 2.23.
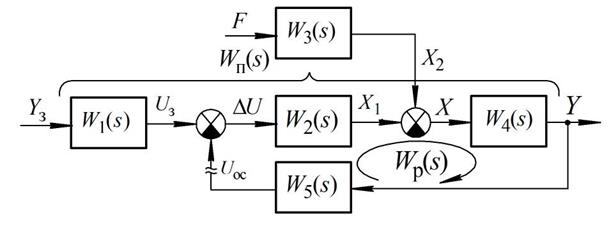
Рис. 2.23 – Узагальнена структура замкнутої САК
Yз(s) - задаючий вплив; Y(s); - керована величина; F(s) – збурюючий вплив;
Uз (s) - сигнал задання; Uос(s) - сигнал зворотного зв'язку;
DU(s) - сигнал неузгодженості; X1(s), X2 (s), X(s), - проміжні сигнали.
Установимо правила еквівалентної заміни наведеної узагальненої схеми більш простою структурою.
Відповідно до рисунка, керована величина залежить як від Yз(s), так і від F(s). Визначимо цю залежність.
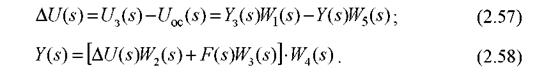
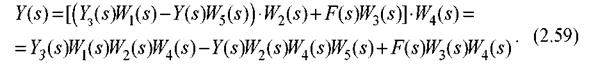
Перетворивши (2.59), одержимо:
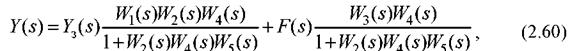
або
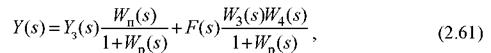
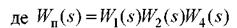передаточна функція прямого ланцюга (еквівалентна передаточна функція між точкою дії задаючого впливу і керованою величиною при розімкнутому контурі зворотного зв'язку;
Wр(s) =W2(s)W4(s)W5(s) - передаточна функція розімкнутого контуру,
одержувана при уявному розмиканні контуру (найчастіше, на ділянці дії сигналу зворотного зв'язку) щодо точок розмикання, обчислена без урахування передатної функції елемента порівняння.
Рівняння (2.61) представимо у вигляді
де YYз (s) - складова керованої величини, обумовлена дією задаючого впливу;
YF (s) - складова керованої величини, обумовлена дією збурюючого впливу. Позначимо:
Величину WY,Yз (s) називають передаточною функцією замкнутої системи за задаючим впливом.
Аналогічно отриману величину
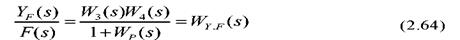
називають передаточною функцією замкнутої системи за збурюючим впливом.
З урахуванням (2.63) і (2.64) рівняння (2.61) набуде вигляду
 |
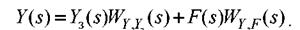Отже вихідна структурна схема може бути представлена в наступному еквівалентному вигляді:
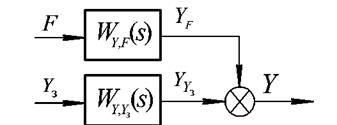
Рис. 2.24 – Еквівалентна структура замкнутої САК
Передаточні функції (2.63) і (2.64) є основними передаточними
функціями САК, тому що вони встановлюють зв'язок керованої величини із вхідними впливами. Якщо ж у процесі розрахунку потрібне визначення передаточної функції замкнутої системи між довільними величинами, то слід застосовувати наступне загальне правило: передаточна функція між
будьякими величинами схеми дорівнює дробу, в якому чисельник є добутком передаточних функцій ланок, включених між точками дії вхідної і вихідної величин, а знаменник – збільшеній на одиницю передаточній функції розі-мкнутого контуру.
Крім функцій (2.63) і (2.64) до основних передаточних функцій
замкнутих САК відносять також функції, що встановлюють зв'язок сигналу неузго-дженості DU(s) з вхідними впливами. Застосувавши загальне правило,
одержимо:
- для передаточної функції за сигналом похибки, викликаним задаючим впливом
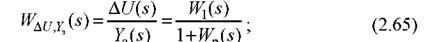
- для передаточної функції за сигналом похибки, викликаним збурюючим впливом
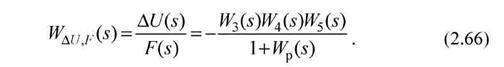
Приклад 2.7. Перетворити до одноконтурного вигляду і визначити основні передаточні функції САК, наведеної на рис. 2.25.
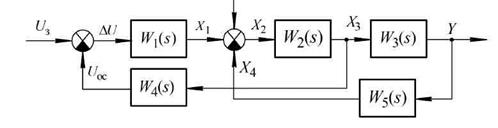
Рис. 2.25 – Вихідна структура САК
Вирішення.
Перенесемо вузол розгалуження сигналу X3 через ланку W3(s) вперед і поміняємо його місцем з вузлом розгалуження сигналу Y див. рис. 2.26.
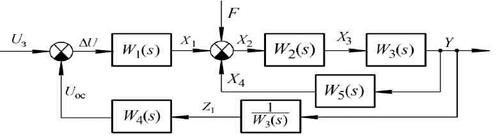
Рис. 2.26
Замінимо другий блок порівняння на еквівалентне з'єднання двох більш простих аналогічних блоків див. рис. 2.27.
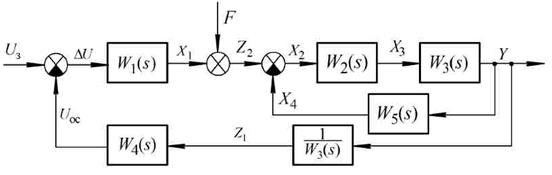
Рис 2.27
Тоді еквівалентна одноконтурна структура САУ може бути подана у вигляді, наведеному на рис. 2.28.
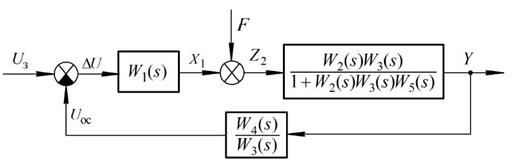
Рис. 2.28 – Еквівалентна структура САК
Передаточні функції системи мають вигляд
Відмітимо, що варіантів перетворення структурних схем завжди існує декілька. У нашому випадку, наприклад, можна спочатку перенести перший блок підсумовування через ланку W1(s), а потім блоки підсумовування
поміняти місцями.
Приклад 2.8. Нехай структурна схема САК має вигляд, наведений на рис. 2.29
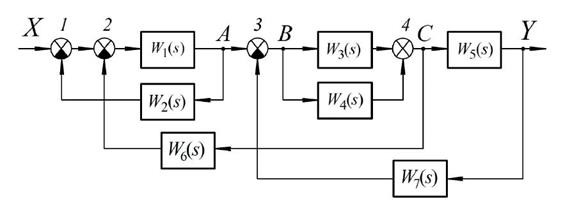
Рис. 2.29 – Вихідна структура САК
Знайдемо передаточну функцію замкнутої системи за задаючим впливом.
Вирішення.
Застосувавши правило перестановки суматорів 1 і 2 і перенісши вузол D з виходу на вхід п'ятої ланки W5 (s), а потім переставивши його з вузлом
C, одержимо структурну схему без перехресних зв'язків.
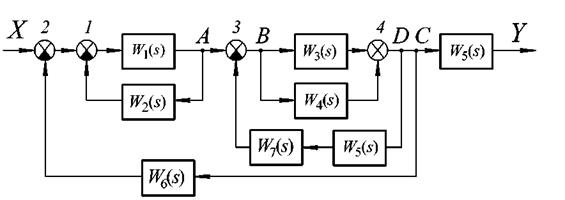
Рис. 2.23 – Еквівалентна структура САК
Скориставшись формулами (2.54) - (2.56) для перетвореної схеми можемо послідовно записати:
