Тогда физический смысл модуля Юнга заключается в следующем: он равен напряжению, соответствующему увеличению длины стержня вдвое, если бы при такой нагрузке тело оставалось упругим и подчинялось бы закону Гука. Действительно, 
численно равно 
при 
, т.е. при 
.
На самом деле подавляющее большинство материалов разрывается раньше, чем они будут растянуты вдвое, поэтому фактически к стальному стержню нельзя приложить напряжение, равное модулю Юнга. Но это совсем не означает, что его вообще нельзя определить на опыте. В данной работе используется один из косвенных методов определения этой одной из важных характеристик упругих свойств тел. В частности, от величины этого модуля зависит энергия и плотность энергии упруго деформированных тел иди сред. Величины модуля Юнга приводятся для разных материалов в справочных таблицах, для стали и железа он равен 
Па или 
.
Можно связать полученные выражения и с той формой закона, которая изучается в школе.
Из (1), (2) и (3) имеем:
| (7) |
Коэффициент 
называют упругостью (для пружин -- жесткостью):
Для стержней этот коэффициент можно рассчитать, для пружин определяется из опыта. (Деформация проволоки в пружине имеет сложный характер и не может быть сведена только к растяжению.) Упругость (жесткость) определяется только упругими свойствами тела и его первоначальными размерами 
, 
.
Часто выражение (7) записывают в проекции на ось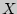 
:
при этом, если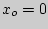 
| (8) |
Сила упругости прямо пропорциональна абсолютному удлинению. Направление силы упругости противоположно направлению внешней растягивающей или сжимающей силы.
Сила упругости. Закон Гука
Виды деформаций
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.
Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, - пластическими.
Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба, кручения и сдвига.
Силы упругости
При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.
Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Природа упругих сил электрическая.
Мы рассмотрим случай возникновения сил упругости при одностороннем растяжении и сжатии твердого тела.
Закон Гука
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид
f=-kx, (2.9)
где f - сила упругости; х - удлинение (деформация) тела; k - коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ - ньютон на метр (Н/м).
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
Рассмотрим опыт, иллюстрирующий закон Гука. Пусть ось симметрии цилиндрической пружины совпадает с прямой Ах (рис. 20, а). Один конец пружины закреплен в опоре в точке А, а второй свободен и к нему прикреплено тело М. Когда пружина не деформирована, ее свободный конец находится в точке С. Эту точку примет за начало отсчета координаты х, определяющей положение свободного конца пружины.
Растянем пружину так, чтобы ее свободный конец находился в точке D, координата которой х>0: В этой точке пружина действует на тело М упругой силой
fх=-kx<0.
Сожмем теперь пружину так, чтобы ее свободный конец находился в точке В, координата которой х<0. В этой точке пружина действует на тело М упругой силой
fх=-kx>0.
Из рисунка видно, что проекция силы упругости пружины на ось Ах всегда имеет знак, противоположный знаку координаты х, так как сила упругости направлена всегда к положению равновесия С. На рис. 20, б изображен график закона Гука. На оси абсцисс откладывают значения удлинения х пружины, а на оси ординат - значения силы упругости. Зависимость fх от х линейная, поэтому график представляет собой прямую, проходящую через начало координат.
Рассмотрим еще один опыт.
Пусть один конец тонкой стальной проволоки закреплен на кронштейне, а к другому концу подвешен груз, вес которого является внешней растягивающей силой F, действующей на проволоку перпендикулярно ее поперечному сечению (рис. 21).
Действие этой силы на проволоку зависит не только от модуля силы F, но и от площади поперечного сечения проволоки S.
Под действием приложенной к ней внешней силы проволока деформируется, растягивается. При не слишком большом растяжении эта деформация является упругой. В упруго деформированной проволоке возникает сила упругости fуп.
Согласно третьему закону Ньютона, сила упругости равна по модулю и противоположна по направлению внешней силе, действующей на тело, т. е.
fуп= -F (2.10)
Состояние упруго деформированного тела характеризуют величиной s, называемой нормальным механическим напряжением (или, для краткости, просто нормальным напряжением). Нормальное напряжение s равно отношению модуля силы упругости к площади поперечного сечения тела:
s=fуп/S (2.11)
Пусть первоначальная длина нерастянутой проволоки составляла L0. После приложения силы F проволока растянулась и ее длина стала равной L. Величину DL=L-L0 называют абсолютным удлинением проволоки. Величину
e=DL/L0 (2.12)
называют относительным удлинением тела. Для деформации растяжения e>0, для деформации сжатия e<0.
Наблюдения показывают, что при небольших деформациях нормальное напряжение s пропорционально относительному удлинению e:
s=E|e|. (2.13)
Формула (2.13) является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным. Коэффициент пропорциональности Е в законе Гука называется модулем продольной упругости (модулем Юнга).
Установим физический смысл модуля Юнга. Как видно из формулы (2.12), e=1 и L=2L0 при DL=L0. Из формулы (2.13) следует, что в этом случае s=Е. Следовательно, модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза. (если бы для такой большой деформации выполнялся закон Гука). Из формулы (2.13) видно также, что в СИ модуль Юнга выражают в паскалях (1 Па = 1 Н/м2).
Диаграмма растяжения
Используя формулу (2.13), по экспериментальным значениям относительного удлинения e можно вычислить соответствующие им значения нормального напряжения s, возникающего в деформированном теле, и построить график зависимости s от e. Этот график называют диаграммой растяжения. Подобный график для металлического образца изображен на рис. 22. На участке 0-1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения sп, при котором еще выполняется закон Гука, называют пределом пропорциональности.
При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1-2), хотя упругие свойства тела еще сохраняются. Максимальное значение sу нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2-3) приводит к тому, что деформация становится остаточной.
Затем образец начинает удлиняться практически при постоянном напряжении (участок 3-4 графика). Это явление называют текучестью материала. Нормальное напряжение sт, при котором остаточная деформация достигает заданного значения, называют пределом текучести.
При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4-5 графика). Максимальное значение нормального напряжения sпр, при превышении которого происходит разрыв образца, называют пределом прочности.
