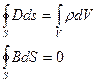
Источниками электрического поля могут быть либо электрические
заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле, всегда связана с порождаемым им магнитным, т. е. электрическое и магнитное поле неразрывно связаны друг с другом—они образуют единое электромагнитное поле.
Тема 15. Вопрос 1.
Свободные (собственные) колебания - это колебания, которые происходят в системе после того, как она была выведена из положения равновесия и предоставлена самой себе. Вынужденные колебания происходят в системе, на которую действует внешняя периодически изменяющаяся сила.
Простейший вид колебаний - это гармонические колебания, при которых смещение x, скорость v и другие характеристики колебания изменяются по закону синуса или - косинуса. Любые колебания возникают в системе, если в ней действует возвращающая сила. Если возвращающая пропорциональна смещению F=kx колебания будут гармоническими. Если эта сила имеет
электромагнитную природу, она называется упругой. Если природа силы иная, ее называют квазиупругой. Общее дифференциальное уравнение свободных гармонических колебаний
имеет вид:
|
Фактически - это II закон Ньютона, что будет ясно из дальнейших примеров.
x -смещение точки от положения равновесия.
 - ускорение колеблющейся точки
|
ω (рад/с) циклическая (круговая) частота колебаний.
Решение этого дифференциального уравнения можно записать как
| смещение точки от положения равновесия |
Учитывая, что скорость υ = dx/dt и ускорение a = dυ/dt и F = -kx, можно получить:
| 
| скорость, колеблющейся точки и ее амплитуда (максимальное значение) |
| 
| ускорение колеблющейся точки и его амплитуда (максимальное значение) |
| 
| возвращающая сила |
| φ - фаза колебания - это не угол, а аргумент, от которого зависит функция смещения x и другие характеристики; φ о - начальная фаза (при t = 0) |
 
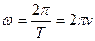
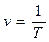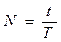
| v (Гц = 1/с) - частота колебаний - это число колебаний за 1 секунду, T (сек) - период колебаний - это время одного полного колебания, N - полное число колебаний, совершенных точкой за, время t. |
| амплитуда колебаний; хо - начальное смещение, υ0 -начальная скорость точки; если υ 0 ≠ 0, амплитуда колебаний будет больше начального смещения. |
| путь, пройденный колеблющейся точкой, N- число полных колебаний, А - амплитуда, t - время колебаний, T -период колебаний |
Тема 15. Вопрос 2.
Пружинный маятник. Это система, состоящая из небольшого тела, подвешенного на легкой пружине и совершающего вертикальные колебания.
| II закон Ньютона, сравнивая с найдем циклическую частоту и период колебаний
| 
|
| В данном случае возвращающая сила - это упругая сила электромагнитной природы, т.е. сила, обусловленная взаимодействием молекул пружины. Выражения для смещения, скорости, ускорения тела - см. ранее. |
Тема 15. Вопрос 3.
Математический маятник. Это тело, подвешенное на легкой нити, размерами которого можно пренебречь по сравнению с длиной нити. Запишем II закон Ньютона в проекции на касательное к траектории (окружности) направление: ma,= - mg sin(a), 
- тангенциальное ускорение. Это уравнение является уравнением колебаний, но не гармонических и имеет более сложно решение, чем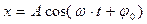 
. Мы рассмотрим только случай малых углов α. При малых углах sin(a) ≡ a ≡ x/l, где l -длина нити.
| II закон Ньютона; сравнивая c , найдем циклическую частоту и период колебаний.
| 
|
| В данном случае возвращающая сила - это составляющая силы тяжести, т.е. сила гравитационной природы, а т.к. при малых углах она пропорциональна смещению, ее можно назвать квазиупругой. |
Тема 15. Вопрос 4.
Физический маятник. Это любое твердое тело, способное совершать колебания относительно неподвижной точки, не совпадающей с его центром тяжести. Если маятник отклонить от положения равновесия, то возникнет возвращающий момент, создаваемый составляющей силы тяжести mg∙sin(α) иравный mg∙sin(a)∙d, где d- плечо силы (см. рис.). Данное тело может совершать только вращательное движение, поэтому II закон Ньютона будет иметь вид: Iε = -mgd; где I - момент инерции тела, а ε - угловое ускорение. Это уравнение колебаний, но не гармонических. Однако при малых углах оно приобретает вид , т.е. дифференциального уравнении гармонических колебаний. При малых углах sin(a) ≡ a ≡ x/d
d - расстояние от точка подвеса до центра тяжести.
угловое ускорение
| 
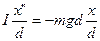II закон Ньютона
| 
| круговая частота и период колебаний физического маятника | |
| уравнение гармонических колебаний |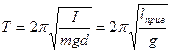 
| ||
| приведенная длина физического маятника. Если взять нить длиной  и подвесить к ней небольшое тело, получим математический маятник, период колебаний которого будет равен периоду колебаний физического маятника.
| |||
Тема 15. Вопрос 5.
смещение точки от положения равновесия
скорость, колеблющейся точки и ее амплитуда (максимальное значение)
ускорение колеблющейся точки и его амплитуда (максимальное значение)
Тема 15. Вопрос 6.
