Найдем индукцию магнитного поля внутри соленоида – катушки, диаметр которой значительно больше ее длины l. Будем считать поле внутри катушки однородным, а вдали от катушки – пренебрежимо малым. Выберем контур обхода L в видепрямоугольника 1-2-3-4 (см. рис.). Найдем сначала циркуляцию вектора В. Запишем интеграл циркуляции в выражение 
. Разобьем интеграл по контуру L на четыре интеграла: 1-2, 2-3, 3-4, 4-1.
|
| В 1-ом интеграле В= const, cos a = 1; во 2-ом - интеграл = 0, т.к. В ^ dl и cos a = 0; третий интеграл = 0, т.к. индукция вне катушки В ® 0; четвертый интеграл = 0 по аналогии со 2-ым. |
Контур 12341 охватывает N витков катушки в каждом из которых ток I. Таким образом, из теоремы следует, что B×l = moNI. Отсюда найдем В.
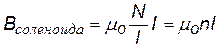
| Магнитная индукция поля внутри длинного соленоида n (1/м)– число витков катушки на единице ее длины |
Тема 9. Вопрос 8.
Поток вектора магнитной индукции (магнитный поток)
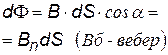
| элементарный поток вектора магнитной индукции В, n – нормаль к площадке, dS – элементарная площадка – это такая малая площадка, в пределах которой B = const; Bn – проекция вектора B на направление нормали n | ||
| поток вектора магнитной индукции (магнитный поток) через конечную площадку S | 
| |
| поток вектора магнитной индукции (магнитный поток) через замкнутую поверхность S | ||
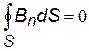
| Теорема Гаусса для индукции магнитного поля: «Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю». |
Представим себе некоторую замкнутую поверхность в магнитном поле. Линии магнитной индукции всегда замкнуты, они не имеют начала и конца, Поэтому количество входящих в поверхность линий будет равно количеству выходящих из нее линий. Магнитный поток пропорционален количеству линий индукции, следовательно, поток будет равен нулю. Равенство нулю магнитного потока через любую замкнутую поверхность свидетельствует о том, что магнитное поле не имеет источников этого поля (магнитных зарядов не существует). Таким образом, магнитное поле является вихревым, т.е. не имеющим источников его образования.
Тема 10. Вопрос 1.
| сила Ампера - действует на проводник dl с током I в магнитном поле; всегда направлена ^ плоскости, в которой лежат dl и В | 
|
Тема 10. Вопрос 2.
Магнитные силы.
Используя выражение для силы Ампера, найдем силу взаимодействия двух бесконечно длинных прямых проводников с токами I1 и I2.
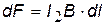
| сила, действующая на элемент dl проводника с током I2 в магнитном поле, создаваемом током I1 (sina = 1, т.к. B ^ dl) В - магнитная индукция поля тока I1 на расстоянии r от него | 
| |
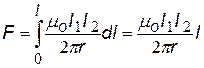
| сила, действующая на проводник длиной l |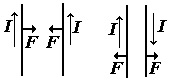 
| |
| сила взаимодействия двух проводников с током в расчете на единицу длины проводника | ||
Мы рассматривали действие проводника с током I1 на проводник с током I2. В соответствии с III законом Ньютона второй проводник действует на первый с такой же силой.
Тема 10. Вопрос 3.
