ѕравильное применение средних возможно лишь на основе предварительной группировки: выделени€ качественно однородных совокупностей и расчленени€ €влени€ на части в зависимости от различи€ условий, под вли€нием которых €вление складываетс€.
ѕод средней величиной в статистике понимают показатель, который характеризует типичный уровень измен€ющегос€ признака в расчете на единицу однородной совокупности в конкретных услови€х места и времени.
ѕри изучении отдельных видов средних величин рекомендуетс€ четко представл€ть методику их расчета и область применени€. Ќаиболее распространенной формой средних величин €вл€етс€ средн€€ арифметическа€, расчет которой производитс€ путем делени€ суммы всех значений изучаемого признака на их количество.
‘ормула расчета:



| å xi | |||||
| x = | , | (5.1) | |||
| n | |||||

где х Ц среднее значение изучаемого признака; xi Цконкретное значение этого признака;
n Цчисло единиц,значение признака которых изучаетс€.


–асчет средней по данной формуле называетс€ способом простой средней арифметической.
≈сли какое-то значение признака повтор€етс€ у нескольких единиц, то в этом случае формула расчета средней арифметической имеет такой вид:
| å x i f i | ||||||
| x = | , | (5.2) | ||||
| å fi | ||||||


 где fi Ц частота повторени€ отдельных вариантов признака.
где fi Ц частота повторени€ отдельных вариантов признака.


ƒанна€ формула носит название средней арифметической взвешенной.
—редн€€ хронологическа€ используетс€ в тех случа€х, когда имеютс€ данные наблюдени€ на определенные моменты времени; ее расчетна€ формула имеет вид:
| = 0.5 x 1 + x 2 + x 3 ++ x n - 1 + 0.5 xn , | ||||
| x | (5.3) | |||
| n -1 | ||||

—редн€€ геометрическа€ используетс€ дл€ анализа темпов роста €влений и вычисл€етс€ по следующим формулам:











| xn | |||||||||
| x = n -1 | , | ||||||||
| x | |||||||||
| x = n -1 k × k × k × | × k | , | |||||||
| n -1 |

где x 1 Ц первый (базисный) уровень р€да динамики; xn Цпоследний уровень р€да динамики;
n Цчисло уровней(или периодов);
k 1, k 2,Е, kn -1Ццепные коэффициенты роста данного р€да динамики.

|
|
|
(5.4)
(5.5)
¬звешенные средние широко примен€ютс€ при обработке данных текущего наблюдени€ по производственным участкам и цехам предпри€ти€, обобщении материалов отчетности предпри€тий и организаций.
—редн€€ гармоническа€ взвешенна€ определ€етс€ по формуле:


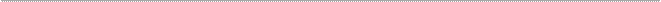



| ’=ћ / (ћ / х), | (5.6) |
где ћ=х∙f


ѕример.
| ѕарти€ | —ебестоимость одной детали, | «атраты на всю партию деталей, |
| деталей | руб. (х) | руб. (ћ) |
| 1,8 | ||
| 2,0 | ||
| 2,3 | ||
’=ћ / (ћ / ’) = (180+400+165) / (180/1,8+400/2+165/2,3) =1,98 (руб.).
—редн€€ себестоимость единицы продукции исчислена по формуле средней гармонической, так как исходной базой исчислени€ средней себестоимости €вл€етс€ отношение затрат на производство всей продукции к количеству единиц продукции.
¬ыбор вида средней зависит от задачи, сто€щей перед исследователем, и характера исходных данных. ≈сли имеютс€ варианты и частота, то дл€ расчета средней величины примен€етс€ средн€€ арифметическа€. ¬ тех случа€х, когда имеютс€ варианты и произведени€ вариант на частоты (х∙f), а частоты неизвестны, дл€ расчета средней величины используетс€ средн€€ гармоническа€.
—редн€€ гармоническа€ используетс€ в тех случа€х, когда следует исчислить среднюю из величин, обратно пропорциональных изучаемому €влению.
—труктурные средние
ќсобого рода средними, используемыми в экономическом анализе дл€ изучени€ структуры вариационного р€да, €вл€ютс€ мода и медиана.
ћедиана Цэто значение признака у той единицы совокупности,котора€ расположена всередине упор€доченного р€да. ѕо данным интервального вариационного р€да, который предварительно ранжирован, медиану определ€ют по формуле:






| Me = x + d | (0.5å f i)- Sm -1 | , | (5.7) | |
| fm | ||||
где x 0 Ц нижн€€ граница медианного интервала; d Цвеличина медианного интервала;
0.5å fi Ц полусумма частот всех интервалов;
Sm -1Цсумма частот до медианного интервала; fm Ц частота медианного интервала.


≈сли р€д дискретный, то медианой €вл€етс€ срединное значение признака, и применение формулы не требуетс€.
ћода Цэто наиболее часто встречающеес€ значение признака.¬ интервальномвариационном р€ду ее определ€ют по формуле:
| Mo = x 0 | + d | f 2 | - f 1 | , | (5.8) | |||
| (f 2 | - f 1) | +(f | 2- f 3) | |||||




где x 0 Ц нижн€€ граница модального интервала; d Цвеличина модального интервала;
f 2Цчастота модального интервала;
f 1Цчастота интервала,предшествующего модальному; f 3Цчастота интервала,следующего за модальным.


¬ дискретном р€ду мода Ц это вариант признака, имеющий наибольшую частоту.
ѕоказатели вариации
онкретные услови€, в которых находитс€ каждый из изучаемых объектов, а также особенности их собственного развити€ (социальные, экономические и пр.) выражаютс€ соответствующими числовыми уровн€ми статистических показателей. “аким образом, вариаци€, т.е. несовпадение уровней одного и того же показател€ у разных объектов, имеет объективный характер и помогает познать сущность изучаемого €влени€.
|
|
|
ƒл€ измерени€ вариации (колеблемости) признака могут быть использованы следующие показатели вариации: размах вариации, среднее линейное отклонение, дисперси€, среднее квадратическое отклонение и коэффициент вариации. “ри последних показател€ обладают преимуществами, обусловленными их математическими свойствами, перед первыми двум€.
| 1. | –азмах вариации: | R = x max - x min , | (5.9) | ||||||||||||||||||||||||
| å | xi - x | × fi | |||||||||||||||||||||||||
| 2. | —реднее линейное отклонение: | l = | , | (5.10) | |||||||||||||||||||||||
| å fi | |||||||||||||||||||||||||||
| 3. | ƒисперсией называетс€ средний квадрат отклонений вариантов от их средней величины. ‘ормула | ||||||||||||||||||||||||||
| расчета: | |||||||||||||||||||||||||||
| ( | ) | ||||||||||||||||||||||||||
| å | x - x | × f | |||||||||||||||||||||||||
| s 2 | = | i | i | , | (5.11) | ||||||||||||||||||||||
| å fi | |||||||||||||||||||||||||||
| 4. | —реднее квадратическое отклонение представл€ет собой корень квадратный из дисперсии, т.е. | ||||||||||||||||||||||||||
| å xi - | |||||||||||||||||||||||||||
| s = | x | × fi | , | (5.12) | |||||||||||||||||||||||
| å | fi | ||||||||||||||||||||||||||

|
|
|
ѕервые четыре показател€ измер€ют абсолютный размер колеблемости признака и выражаютс€ в тех же единицах измерени€, что и значени€ признака.
оэффициент вариации позвол€ет сравнивать колеблемость (вариацию) различных, но взаимосв€занных €влений (или их признаков), а также колеблемость одноименных признаков, но действующих в различных услови€х места или времени.
‘ормула расчета:
| v = | s | ×100 %, | (5.13) | |
| x |







оэффициент вариации используют не только дл€ сравнени€ оценки вариации единиц совокупности, но и как характеристику однородности совокупности. —овокупность считаетс€ количественно однородной, если коэффициент вариации не превышает 33 %.






