Правило дифференцирования сложной функции

Дифференциальное исчисление

Производная функции

Производной функции у = f (х) в точке х ₀ называется предел отношения приращения функции к приращению аргумента при 0:

y¢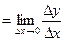

- приращение функции у;

- приращение аргумента х.

 

4.2. Геометрическийсмыслпроизводной

 

Производная функции f(х) в точке х₀ равна тангенсу угла наклона касательной, проведенной к кривой у = f (х) в точке х₀, то есть у¢ = tg a, где a – угол наклона касательной к оси Ох в данной точке.

Уравнениекасательной к данной кривой у = f(х), проходящей через точку на ней М (х₀, у₀) имеет вид:

у – у₀ = f ¢ (х₀) (х – х₀),

где угловой коэффициент k =tg a в точке х₀ и равен производной функции в этой точке.

 

Механический смысл производной

Производная функции – есть мгновенная скорость изменения функции в точке х₀. Возьмем в качестве функции путь S, а в качестве аргумента время t. Средняя скорость движения материальной точки в промежутке времени Dt равна отношению промежутка пути D S к промежутку времени D t. Если устремим промежуток времени к нулю, Dt ®0, то получим мгновенную скорость движения материальной точки и эта мгновенная скорость равна производной от пути по времени. Обозначается это так:

V = S¢ = .

Применение производной в экономических задачах.

В экономической теории существует понятие эластичности, которое было введено А. Маршалом в связи с анализом функций спроса. С математической точки зрения понятие эластичности определяется с помощью понятия производной.

Эластичностью функции ( function elasticity) - называется предел отношения относительного приращения функции y/у к относительному приращению х/х, когда х 0 и у 0. Эластичность обозначается символом Е(у) и выражается формулой:

Е(у)=

 

4.5. Дифференциалфункции

 

Дифференцирование функции – это нахождение (отыскание) производной функции.

Дифференциалом функции у = f(х) называется главная часть её приращения, линейная относительно приращения аргумента. Дифференциалом аргумента dх называется приращение аргумента Dх. Дифференциалфункции равен произведению производной на дифференциал аргумента:

dy = f ¢(x)× dx.

 

Основные правила дифференцирования

1. Производная от суммы (разности) функций u = u(х) и v = v(х) равна сумме (разности) производных этих функций:

(u¢ v¢) = u¢ v¢

2. Постоянный множитель c можно выносить из-под знака производной:

(c• u)¢ = с• u¢

3. Производная от произведения двух функций u = u(х) и v = v (х) вычисляется по формуле:

(uv)¢=u¢• v+u• v¢

4. Производная от частного двух функций вычисляется по формуле:

Правило дифференцирования сложной функции

 

Если у =f (u), а u = u (х), то есть y = y{u (х)}- сложная функция, тогда производная сложной функции находится по формуле:

y¢_x = y¢_u• u¢_x

Пример

Найти производную сложной функции:

у = (х² +5)³

Решение: обозначим у = u³, где u = х² + 5, запишем производные

у¢_u = 3u² u¢_x = 2х, подставим в формулу производной сложной функции:

у¢_х = 3u² 2х = 3(х² + 5)² 2х.

 

4.8. Дифференцирование функций, заданных параметрически.

Пусть функция у = f (х) задана через параметр t, а именно х =х (t) и у=у(t). Тогда производная от функции у по х выражается через производные от функции х по t и от функции у по t:

у¢_x =

 

4.9. Дифференцирование неявно заданной функции.

Для неявно заданных функций нет единой формулы определения производной, а существует метод нахождения производной. Пусть функция у неявно содержится в уравнении F(х,у) = 0. Возьмем производные по х в каждой части уравнения, при этом функцию у будем рассматривать как сложную функцию. Получим уравнение относительно у¢. Из этого уравнения и находим у¢.

Пример

Найти производную у¢ из уравнения х² + у² = 5

Решение

Продифференцируем каждую часть уравнения по х:

2х + 2у у¢= 0, следовательно, у¢ = - х/ у.