У випадку, коли досліджуваний об’єкт або явище характеризується більш ніж двома ознаками Х 1, Х 2, …, Хk, необхідно вивчати множинні залежності. Для оцінки сили зв’язку між певною ознакою Хі та усіма іншими ознаками слугує множинний коефіцієнт кореляції, який позначається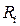 
.
Для розрахунку множинного коефіцієнта кореляції необхідно:
1) Побудувати матрицю парних коефіцієнтів кореляції 
між ознаками 
та 
:
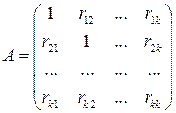. (3.7)
2) Знайти визначник 
матриці А та алгебраїчне доповнення 
елемента 
цієї матриці.
3) Розрахувати множинний коефіцієнт кореляції за формулою:
. (3.8)
Перевірка статистичної значущості множинного коефіцієнта кореляції здійснюється за допомогою t-статистики, яка розраховується за формулою:
(3.9)
де п – кількість взаємопов’язаних значень ознак 
.
Розраховане значення t-статистики порівнюється з критичним значенням Fкрит. Fкрит – табличне значення розподілу Фішера, яке також можна знайти за допомогою вбудованої статистичної функції Excel FРАСПОБР (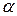
; l 1; l 2), де 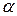– обраний дослідником рівень значущості, l 1; l 2 – ступені волі, l 1= k –1; l 2 = п – k.
Якщо розраховане значення t-статистики більше критичного 
, то множинний коефіцієнт кореляції вважається значимим на обраному рівні значущості .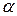
У випадку, коли необхідно дослідити кореляційний зв’язок між ознаками Хі та , 
, 
, із множини ознак Х 1, Х 2, …, Хk досліджуваного об’єкту або явища, вільний від впливу всіх інших ознак, розраховується частинний коефіцієнт кореляції, який позначається 
.
Для розрахунку частинного коефіцієнта кореляції необхідно:
1) Побудувати матрицю парних коефіцієнтів кореляції А.
2) Знайти алгебраїчні доповнення 
елементів 
відповідно.
3) Розрахувати частинний коефіцієнт кореляції за формулою:
. (3.9)
Перевірка статистичної значущості частинного коефіцієнта кореляції здійснюється за допомогою t-статистики, яка розраховується за формулою:
, (3.10)
де п – кількість взаємопов’язаних значень ознак .
Розраховане значення t-статистики порівнюється з критичним значенням tкрит. tкрит – табличне значення розподілу Стьюдента, яке також можна знайти за допомогою вбудованої статистичної функції Excel СТЬЮДРАСПОБР (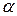; l), де 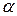– обраний дослідником рівень значущості, l – ступені волі, l = п – k +2.
Якщо розраховане значення t-статистики більше критичного 
, то частинний коефіцієнт кореляції вважається значимим на обраному рівні значущості .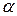
Зауваження. 1. Вважається, що для коректного використання множинного і частинного коефіцієнтів кореляції необхідно, щоб вибіркові дані мали сумісний нормальний розподіл, однак перевірка цієї умови на практиці зазвичай не виконується, оскільки пов’язана зі значними труднощами у розрахунках.
2. Замість парного коефіцієнта кореляції Пірсона можна використовувати також парний коефіцієнт кореляції Спірмена.
3. Кореляційна матриця завжди симетрична відносно головної діагоналі, оскільки 
. Елементи головної діагоналі завжди дорівнюють 1, оскільки вони є коефіцієнтами кореляції та .
Завдання для самостійного виконання
1. Визначити силу зв’язку між вагою рослини X (г) і вагою його насіння Y (г) за даними таблиці 1
Таблиця 1
| X | |||||||
| Y |
2. В таблиці 2 приведені дані про роздрібний товарообіг Z (млрд. грн.), середню кількість населення X (млн. осіб) та середній доход Y (млн. грн.). Проаналізувати зв’язок між Z та X і Y за частинними і множинним коефіцієнтами кореляції.
Таблиця 2
| Z | 1,2 | 1,3 | 2,5 | 1,4 | 1,2 | 0,2 | 2,4 | 4,1 | 1,1 |
| X | 1,4 | 1,4 | 2,5 | 1,5 | 1,3 | 0,3 | 2,6 | 4,2 | 1,1 |
| Y | 1,3 | 1,3 | 1,4 | 1,8 | 1,5 | 1,6 | 1,8 | 1,9 | 1,6 |
3. Для дослідження впливу капіталовкладень X (млн. грн.) на отриманий річний прибуток Y (млн. грн.) було зібрано статистичні дані за 20 крупними підприємствами (табл.3). Визначити силу зв’язку між означеними факторами.
Таблиця 3
| X Y | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| 1,5 – 2,5 | - | - | - | - | |
| 2,5 – 3,5 | - | - | |||
| 3,5 – 4,5 | - | - | |||
| 4,5 – 5,5 | - | - | - | - |
4. В таблиці 4 приведені дані про щомісячний прибуток Z (тис. у. од.), витрати на рекламу X (тис. у. од.) та вкладення капіталу в цінні папери Y (тис. у. од.). Проаналізувати зв’язок між Z та X і Y за частинними і множинним коефіцієнтами кореляції.
Таблиця 4
| Z | |||||||
| X | 0,2 | 0,5 | 0,3 | 0,5 | 0,5 | 0,6 | 0,8 |
| Y | 0,8 | 0,2 | 1,2 | 0,9 | 1,1 |
5. В таблиці5 наведено дані про рівень витрат X (%) та річний доход Y (млн. грн.), які було зібрано за 50 крупними магазинами. Визначити силу зв’язку між означеними факторами.
Таблиця 5
| X Y | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 | 12 – 14 |
| 0,5 – 2,0 | - | - | |||
| 2,0 – 3,5 | - | - | |||
| 3,5 – 5,0 | - | - | |||
| 5,0 – 6,5 | - | - | |||
| 6,5 – 8,0 | - | - | - |
6-9. За даними таблиці 6 перевірити гіпотезу про наявність лінійного зв’язку.
Таблиця 6
| № | X | Y |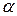
| ||||||||
| 0,05 | |||||||||||
| 0,01 | |||||||||||
| 0,05 | |||||||||||
| 0,01 |
