Для оцінки сили зв’язку між Х та Y у випадку, коли між Х та Y існує нелінійний зв’язок або вибіркові дані не розподілені за нормальним законом, слугує коефіцієнт кореляції Спірмена.
Коефіцієнт кореляції Спірмена розраховується за формулою:
, (3.5)
де п – кількість пар вибіркових даних;
– різність між рангами і -го значення Х та відповідного значення Y;
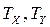– поправки, що пов’язані з однаковими рангами; розраховуються за формулами:
; 
, (3.6)
де 
– кількість зв’язок (груп однакових рангів);
– розміри і-тих зв’язок (кількість елементів в них).
Зауваження 1. Ранги присвоюються вибірковим даним звичайним способом (див. п. 2.3.4).
Зауваження 2. Статистична значущість коефіцієнта кореляції Спірмена перевіряється так, як й коефіцієнта кореляції Пірсона.
ПРИКЛАД 3.3. Вивчається залежність між продуктивністю праці робітників Х (тис. грн.) та їх емоційним відношенням до своєї професійної діяльності Y (бали). Відповідні дані подано у таблиці 3.8. Оцінити силу зв’язку між досліджуваними факторами за коефіцієнтом кореляції Спірмена. Перевірити його статистичну значущість.
Таблиця 3.8
| Х | |||||||||||||||
| Y |
Розв’язок. Дані таблиці 3.8 є вибірковими парами значень 
, 
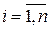; п – кількість пар, п =15. Знайдемо коефіцієнт кореляції Спірмена, необхідні розрахунки оформимо у вигляді таблиці (табл. 3.9), використовуючи позначення: 
– ранг хі, 
– ранг уі.
Таблиця 3.9
| хі | |||||||||||||||
| yі | |||||||||||||||
|
| 4,5 | 8,5 | 4,5 | 8,5 | |||||||||||
|
| 2,5 | 2,5 | |||||||||||||
 і
| -1 | -2 | 2,5 | 0,5 | -4 | -4 | 0,5 | 5,5 | |||||||
| і 2
| 6,25 | 0,25 | 0,25 | 30,25 |
Пояснимо, як заповнюється рядок 3: знаходимо найменше зі значень хі (це 26) та присвоюємо йому ранг 1; знаходимо наступне найменше (це 28) і присвоюємо йому ранг 2; наступним найменшим є 31, йому присвоюємо ранг 3; наступними найменшими є два значення 32, якщо б вони були різними, то їм би присвоїли ранги 4 і 5, але оскільки вони однакові, то присвоюємо їм середній ранг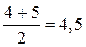 
; і т.д.
Знаходимо суму квадратів різностей рангів: 
=1+4+1+6,25+ +0,25+16+16+1+0,25+30,25=76.
Знаходимо поправки, що пов’язані з однаковими рангами. В ряду рангів є дві групи однакових рангів, в перший з них 2 елемента, в другій теж два. Отже, 
, 
.
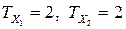В ряду рангів є дві групи однакових рангів, в перший з них 2 елемента, в другій три елемента. Отже,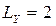 
, 
.
Підставимо отримані дані в формули (3.6) і знайдемо поправки:
;
.
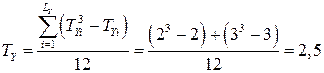Знайдемо коефіцієнт кореляції Спірмена за формулою (3.6):
.
За значенням коефіцієнта кореляції можна зробити висновок, що між Х та Y існує сильний додатній зв’язок.
Перевіримо статистичну значущість знайденого коефіцієнта кореляції. Розрахуємо t-статистику за формулою (3.4): 
. Знайдемо tкрит, враховуючи, що l = п -2=15-2=13. Оберемо рівень значущості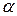 
=0,001. Тоді tкрит =СТЬЮДРАСПОБР (0,001; 13)=4,22.
Оскільки розраховане значення t-статистики більше критичного 
, то коефіцієнт кореляції можна вважати значимим на обраному рівні 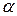=0,001.
Висновок. Між продуктивністю праці та емоційним відношенням працівника до професійної діяльності існує сильний додатній зв’язок. Висновок дійсний для всієї генеральної сукупності, з якої було зроблено вибірку.
