Лабораторна робота №3
Основи кореляційного аналізу
Поняття кореляційного зв’язку між досліджуваними величинами
В багатьох прикладних задачах необхідно виявити залежність між двома властивостями (ознаками) Х і Y одного і того ж економічного об'єкту, або між певними ознаками різних об’єктів. Якщо вказані ознаки допускають кількісне вимірювання, і, з погляду економічної теорії, виходячи з економічної характеристики об'єкту, ознака Y залежить від ознаки Х, тоді Х можна назвати незалежною змінною, або факторною ознакою, або просто фактором, а Y – залежною змінною або результативною ознакою.
Якщо кожному значенню факторної ознаки Х відповідає одне і тільки одне значення результативної ознаки Y, то говорять, що між цими ознаками існує функціональний зв’язок: Y = f (Х).
Якщо кожному значенню факторної ознаки Х відповідає безліч значень результативної ознаки Y, то говорять, що між цими ознаками існує статистичний зв’язок.
Наприклад, якщо Х приймає l значень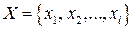 
і кожному її значенню хі відповідає множина значень Y, тобто:
значенню х 1 відповідає множина 
;
значенню х 2 відповідає множина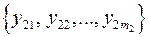 
;
…
значенню хl відповідає множина 
;
то між Х та Y існує статистичний зв’язок.
Вивчення статистичного зв'язку дуже складний і трудомісткий процес, у якому потрібно аналізувати багатомірні таблиці даних. Тому зазвичай вивчається не статистичний, а кореляційний зв'язок між Х та Y.
Якщо кожному значенню факторної ознаки Х відповідає певне середнє значення результативної ознаки Y, то говорять, що між цими ознаками існує кореляційний зв’язок. Тобто кореляційною є функціональна залежність між значеннями Х і середніми значеннями Y: 
= f (Х). Наприклад, якщо Х приймає l значень 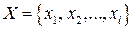і кожному її значенню хі відповідає середнє множини значень Y, тобто:
значенню х 1 відповідає 
;
значенню х 2 відповідає 
;
…
значенню хl відповідає 
;
то між Х та Y існує кореляційний зв’язок.
Наприклад відомо, що з однакових за площею ділянок землі при рівних кількостях внесеного добриву отримують різний урожай. Тому, якщо Y – урожайність зерна, а Х – кількість внесеного добриву, то функціонального зв’язку між Х та Y немає. Це пояснюється впливом таких випадкових факторів, як температура повітря, кількість опадів і т. ін. Однак досвід показує, що середній урожай є функцією від кількості добриву, тобто між Х та Y існує кореляційний зв’язок.
Основними задачами кореляційного аналізу є:
- вивчення сили зв’язку між двома і більше ознаками досліджуваного об’єкту;
- встановлення факторів, що найбільш суттєво впливають на результативну ознаку;
- виявлення невідомих причинно-наслідкових зв’язків між ознаками об’єкту.
