Касательная к графику функции

Приращение функции

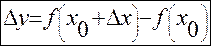
По графикам функций, представленных на рисунках, найдите приращение аргумента и приращение функ­ции при переходе от точки к точке :

1.1) 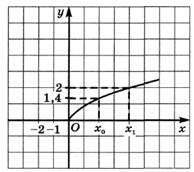1.2)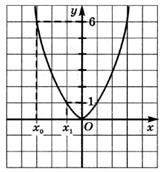

Найдите приращение функции 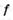в точке 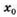, если:

1.3) ;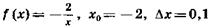

1.4) ;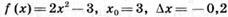

1.5) ;

1.6)

1.7) ;

1.8) ;

1.9) ;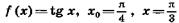

1.10)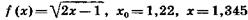

 

Найдите приращение функции при переходе от
точки к точке 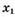, если:

1.11)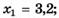

1.12)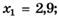

1.13)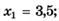

1.14)

 

Найдите приращение функции 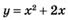при переходе от
точки 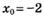к точке 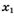, если:

1.15)

1.16)

1.17)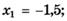

1.18)

 

Найдите приращение функции 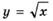при переходе от

точки 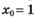к точке , если:

1.19)

1.20)

1.21)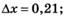

1.22)

 

Найдите приращение функции при переходе от
точки 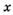к точке , если:

1.23)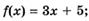

1.24)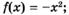

1.25)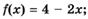

1.26)

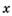Для функции найдите при переходе от точки к
точке 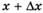, если:

1.27)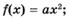

1.28)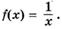

 

Ответы

	Δ y = –0,6; Δ x = –2		–0,19
	Δ y = –5; Δ x = 2		0,21
	1/19		–0,75
	–2,32		1,25
	0,03		0,2
	0,205		–0,1
	1/4		0,1
	–2/5		0,05
			3Δ x
	1/10		–2 x Δ x – (Δ x)2
	0,4		–2Δ x
	–0,2		4 x Δ x + 2(Δ x)2
			2 ax Δ x + a (Δ x)2
	–1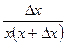

 

Вычисление производных

 

Правила дифференцирования (и, v, w — функции аргумента х, по которому производится дифференцирование).

1. Производная алгебраической суммы

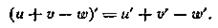
2. Производная произведения

В частности, если С — постоянная, то

3. Производная частного (дроби)

В частности,

10Таблица основных формул дифференцирования

№ п/п	Функция	Производная	№ п/п	Функция	Производная
	C (постоянная)			sin x	cos x
	(α – постоянная)			cos x	–sin x
	Частные случаи:			tg x
	x			ctg x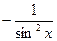
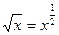
				arcsin x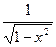
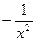
				arccos x
	ax (a > 0 – постоянная)	ax ln a		arctg x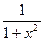
	ex	ex		arcctg x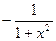
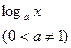
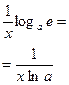
				xx	xx (1 + ln x)
	ln x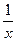
	lg x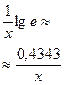

 

4. Производная сложной функции (функции от функции).

Если

Если u – функция от x и a – постоянная, то:

 

Найдите производную функции

2.1) .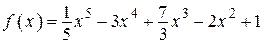

 

2.2)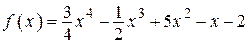

2.3)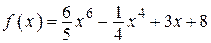

 

2.4)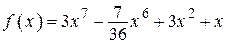

 

2.5)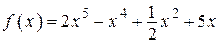

 

2.6)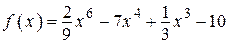

 

2.7)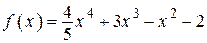

2.8)

2.9) .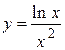

2.10) .

 

2.11) .

 

2.12) .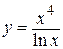

 

2.13) .

2.14) .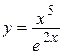

 

2.15) .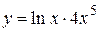

 

2.16) .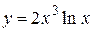

 

2.17) .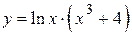

 

2.18) .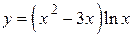

 

2.19) .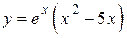

 

2.20) .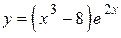

 

2.21) .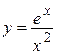

 

2.22) .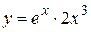

 

 

2.23) .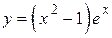

 

2.24) .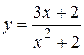

2.25) .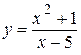

 

2.26) .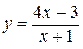

 

2.27) .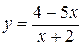

 

2.28) .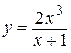

 

2.29) .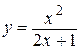

 

2.30) .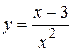

 

2.31) .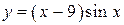

 

 

2.32) .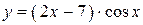

 

2.33) .

 

2.34) .

 

2.35) .

 

2.36) .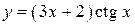

 

2.37) .

 

2.38) .

 

2.39) .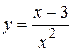

 

2.40) .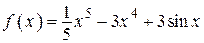

2.41) .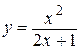

 

2.42) .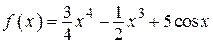

2.43) .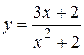

2.44) .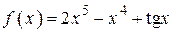

2.45) .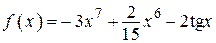

2.46) .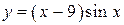

 

2.47) .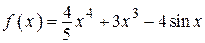

2.48) .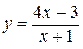

 

2.49) .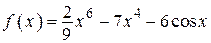

2.50) .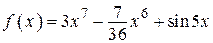

2.51) .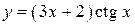

 

2.52) .

 

2.53) .

2.54) .

 

2.55) .

 

2.56) .

 

2.57) .

 

2.58) .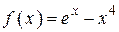

 

2.59) .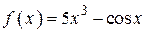

 

2.60) .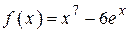

 

2.61) .

 

2.62) .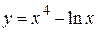

 

2.63) .

 

2.64) .

 

2.65) .

2.66) .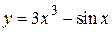

 

2.67) .

 

2.68) .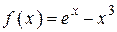

 

2.69) .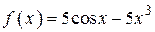

2.70) .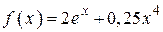

2.71) .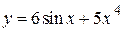

 

2.72) .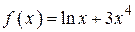

2.73) .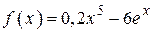

 

2.74) .

 

2.75) .

 

2.76) .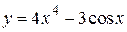

 

2.77) .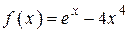

 

2.78) .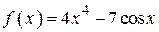

 

2.79) .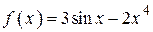

 

2.80) .

 

2.81) .

 

2.82) .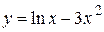

 

2.83) .

 

2.84) .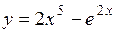

2.85) .

2.86) .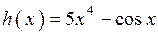

2.87) .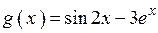

2.88) .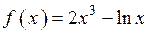

 

2.89) .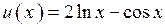

2.90) .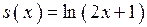

2.91) .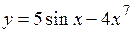

 

2.92) .

2.93) .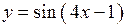

2.94) .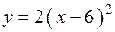

2.95) .

2.96) .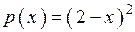

2.97) .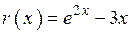

2.98) .

2.99) .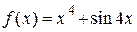

 

2.100) .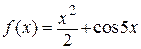

2.101) .

2.102) .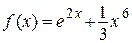

2.103) .

2.104) .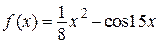

2.105) .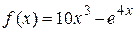

2.106) .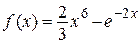

2.107) .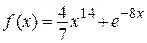

2.108) .

2.109) .

2.110) .

2.111) .

2.112) .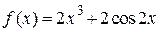

2.113) .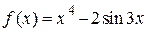

2.114) Вычислите значение производной функции 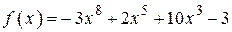в точке .

 

 

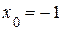2.115) Вычислите значение производной функции 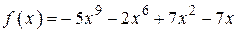в точке .

 

 

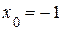2.116) Вычислите значение производной функции 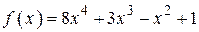в точке .

 

 

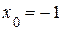2.117) Вычислите значение производной функции в точке .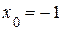

 

 

2.118) Вычислите значение производной функции 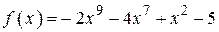в точке .

 

 

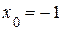2.119) Вычислите значение производной функции 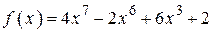в точке .

 

 

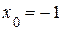2.120) Вычислите значение производной функции 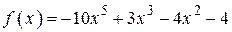в точке .

 

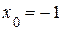Ответы

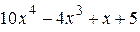
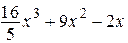
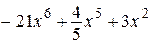
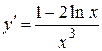
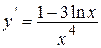
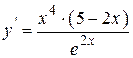
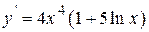
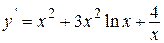
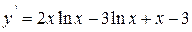
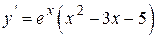
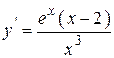
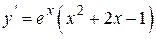
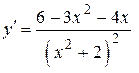
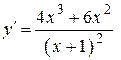
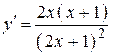
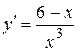
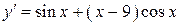
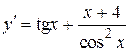
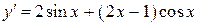
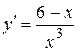
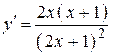
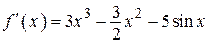
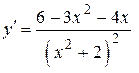
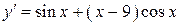
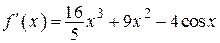
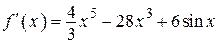
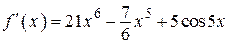
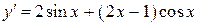
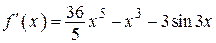
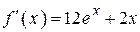
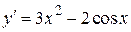
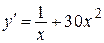
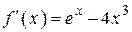
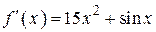
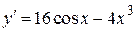
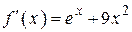
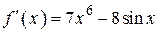
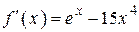
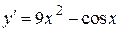
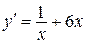
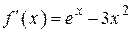
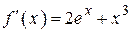
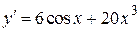
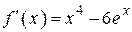
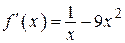
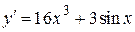
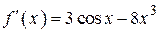
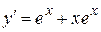
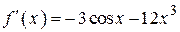
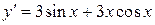
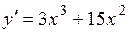
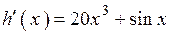
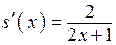
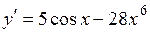
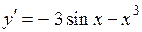
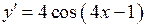
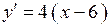
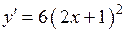
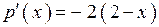
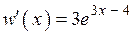
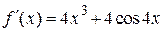
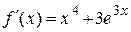
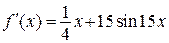
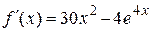
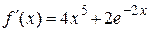
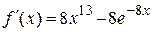
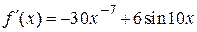
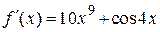
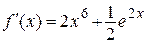
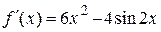
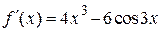
	–54
	–21
	–37
	–48
	–33

 

Касательная к графику функции

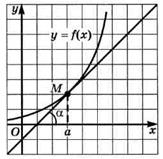
Геометрический смысл производной состоит в следующем. Если к графику функции у = f (x)в точке с абсциссой х = а можно провести касательную, непараллельную оси у, то выражает угловой коэф-

фициент касательной:

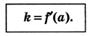
Поскольку 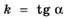, то верно равенство

 

 

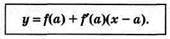
Составьте уравнение касательной к графику функции в точке с абсциссой , если:

3.1)

3.2)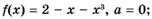

3.3)

3.4)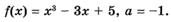

3.5)

3.6)

3.7)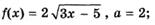

3.8)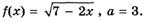

3.9)

3.10)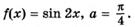

3.11)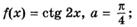

3.12)

3.13) Найдите тангенс угла наклона касательной, проведенной к графику функции 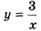в точке с абсциссой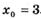

3.14) Найдите тангенс угла наклона касательной, проведенной к графику функции 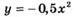в точке с абсциссой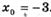

3.15) Найдите угловой коэффициент касательной, проведенной к графику функции 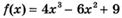через его точку с абсциссой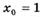

3.16) Найдите тангенс угла наклона касательной, проведенной к графику функции 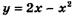в точке с абсциссой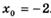

3.17) Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой

3.18) Найдите угловой коэффициент касательной, проведенной
к графику функции 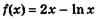в точке с абсциссой

 

 

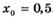
3.19) Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

3.20) Найдите угловой коэффициент касательной к графику функ­ции 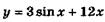в точке с абсциссой

3.21) К графику функции в точке с абсциссой 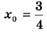проведена касательная. Найдите тангенс угла накло­на касательной к оси Ох.

 

3.22) Напишите уравнения касательных к графику функции
в точках его пересечения с осью абсцисс.

 

3.23) Напишите уравнения касательных к параболе
в точках с ординатой 4.

 

3.24) На графике функции найдите точки,
в которых касательная образует с положительным
направлением оси абсцисс угол . Составьте уравнение
каждой из этих касательных.

 

В какой точке касательная к графику функции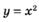
параллельна заданной прямой:

3.25)

3.26)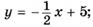

3.27)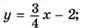

3.28)

 

В каких точках касательная к графику заданной функ­ции параллельна заданной прямой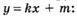

 

3.29)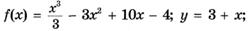

3.30)

3.31)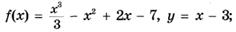

3.32)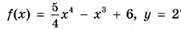

3.33)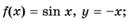

3.34)

3.35)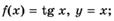

3.36)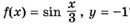

 

Напишите уравнения тех касательных к графику функции , которые параллельны заданной прямой:

3.37)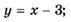

3.38)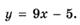

 

3.39) Определите абсциссу точки, в которой касательная к графику функции 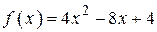параллельна оси абсцисс.

 

3.40) Найдите абсциссу точки графика функции 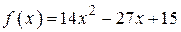, в которой касательная наклонена под углом к оси абсцисс.

 

3.41) Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .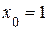

 

3.42) Найдите угол наклона касательной, проведенной к графику функции в точке с абсциссой .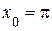

3.43) Найдите угол между касательной к графику функции 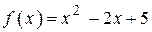в точке с абсциссой и осью абсцисс.

3.44) К графику функции 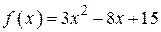проведена касательная параллельно прямой . Найдите абсциссу точки касания.

 

3.45) К графику функции 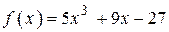в точке с абсциссой 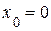проведена касательная. Найдите абсциссу точки пересечения этой касательной с осью ОХ.

 

3.46) На графике функции 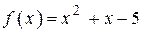взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.

 

3.47) Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .

3.48) К графику функции в точке с абсциссой 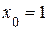проведена касательная. Найдите абсциссу точки графика касательной, ордината которой равна 31.

3.49) Найдите абсциссу точки, в которой касательная к графику функции 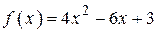параллельна прямой .

 

3.50) К графику функции в точке с абсциссой 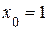проведена касательная. Найдите абсциссу точки пересечения касательной с осью ОХ.

 

3.51) Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой 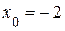. 67

3.52) Через точку графика функции 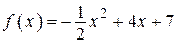с абсциссой 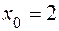проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.

 

3.53) Определите угол, который образует касательная, проведенная к графику функции в точке с абсциссой , с положительным направлением оси Ox.

 

3.54) Функция 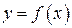определена на промежутке . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции 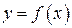имеет наибольший угловой коэффициент.

 

3.55) Функция 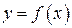определена на промежутке 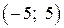. На рисунке изображен график производной этой функции.

К графику функции провели касательные во всех точках, абсциссы которых ‑ целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.

 

3.56) Прямая пересекает ось абсцисс при 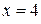, касается графика функции в точке . Найдите .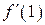

 

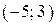3.57) Функция определена на промежутке . Используя изображенный на рисунке график производной , определите количество касательных к графику функции , которые составляют угол с положительным направлением оси Ox.

 

3.58) Функция 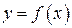определена на промежутке 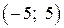. На рисунке изображен график производной этой функции.

К графику функции провели касательные во всех точках, абсциссы которых ‑ целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.

 

3.59) Функция определена на промежутке . На рисунке изображен график производной . Определите число касательных к графику функции , тангенс угла наклона которых к положительному направлению оси Ox равен 3.

 

3.60) Прямая пересекает ось ординат при , касается графика функции в точке . Найдите .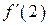

 

3.61) Функция 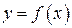определена на промежутке 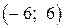. На рисунке изображен график производной этой функции.

К графику функции провели касательные во всех точках, абсциссы которых ‑ целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.

 

3.62) Прямая пересекает ось ординат при 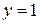, касается графика функции в точке 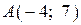. Найдите .

 

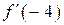3.63) Функция определена на промежутке . Используя изображенный на рисунке график производной , определите количество касательных к графику функции , которые составляют угол 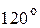с положительным направлением оси Ox.

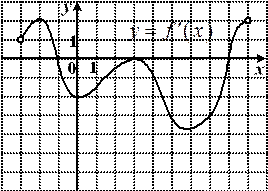
3.64) Функция 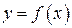определена на промежутке . На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции имеет наибольший угловой коэффициент.

 

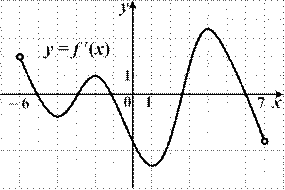
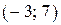3.65) Функция определена на промежутке . Используя изображенный на рисунке график производной , определите количество касательных к графику функции , которые составляют угол 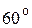с положительным направлением

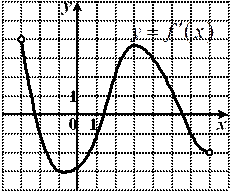оси Ox.

 

3.66) Прямая пересекает ось абсцисс при , касается графика функции