Завдання №1
| Що робити | Чим керуватися |
| 1. Перекреслити умову завдання |

|
| 2. Виконати аналіз навантаження балки | Визначити тип балки, позначити опори, використовуючи принцип звільнення, виявити реакції опор балки, перерахувати навантаження, що діють |
| 3. Викреслити розрахункову схему балки (відкинути тіло від зв'язків і зобразити задані сили, що діють на нього, і реакції відкинутих зв'язків) |

|
| 4. Вибрати систему координат і скласти рівняння рівноваги |
Початок координат сумістити з лівим краєм балки, вісь Х направити уздовж балки
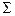 Fx = 0; RXB = 0 (1) Fx = 0; RXB = 0 (1)
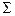 MA = 0; -F 3 – M + q4 8 – RYB 10 = 0 (2) MA = 0; -F 3 – M + q4 8 – RYB 10 = 0 (2)
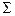 MB = 0; - F 13 + RYA 10 – M – q4 2 = 0 (3) MB = 0; - F 13 + RYA 10 – M – q4 2 = 0 (3)
|
| 5. Визначити шукані величини |
З рівняння (1)
RXB = 0
З рівняння (2)
RYB=  З рівняння (3)
RYA
З рівняння (3)
RYA 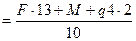
|
| 6. Перевірити правильність отриманих результатів по рівнянню, яке не було використано при розв'язуванні задачі |

|
Завдання №2
| Що робити | Чим керуватися |
| 1. Перекреслити умову завдання | 
|
| 2. Виконати аналіз навантаження балки | Визначити тип балки, позначити опори, використовуючи принцип звільнення, виявити реакції опор балки, перерахувати навантаження, що діють |
| 3. Викреслити розрахункову схему балки (відкинути тіло від зв'язків і зобразити задані сили, що діють на нього, і реакції відкинутих зв'язків) | 
|
| 4. Вибрати систему координат і скласти рівняння рівноваги |
Початок координат сумістити з лівим краєм балки, вісь Х направити уздовж балки
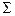 Fx = 0; Rx = 0 (1) Fx = 0; Rx = 0 (1)
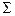 Fy = 0; Ry - F - q4 = 0 (2) Fy = 0; Ry - F - q4 = 0 (2)
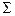 MA = 0; MR + F 3 – M + q4 11 = 0 (3) MA = 0; MR + F 3 – M + q4 11 = 0 (3)
|
| 5. Визначити шукані величини | З рівняння (1) Rx = 0 З рівняння (2) Ry = F + q4 З рівняння (3) MR = - F 3 + M - q4 11 |
| 6. Перевірити вірність отриманих результатів по рівнянню, яке не було використано при розв'язуванні задачі |
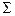 MB = MR + Ry 13 - F 10 – M - q4 2 = 0 MB = MR + Ry 13 - F 10 – M - q4 2 = 0
|
Короткі теоретичні відомості
Опори балок по їх пристрою можуть бути розділені на наступні три основні типи (мал. 1):
1. шарнірно – рухома (опора А);
2. шарнірно – нерухома (опора В);
3. жорстке закладення (опора С).

Малюнок 2
Застосуємо правило для визначення напряму реакцій зв'язків: напрям реакції зв'язку протилежний напряму переміщення, що знищується даним зв'язком.
Шарнірно-рухома опора допускає поворот навколо осі шарніра і лінійне переміщення паралельно опорній площині. Якщо нехтувати тертям на опорі і в шарнірі, то реакція такого зв'язку буде направлена перпендикулярно опорній площині і невідома тільки по модулю (одне невідоме).
Шарнірно-нерухома опора допускає тільки поворот навколо осі шарніра і не допускає ніяких лінійних переміщень. Реакція такої опори буде направлена перпендикулярно осі шарніра; модуль і напрям її наперед не відомі (два невідомих). Зазвичай при рішенні задач таку реакцію розкладають на дві взаємно перпендикулярні складові, не відомі по модулю, але відомі по напряму.
Жорстке закладення (затискання) не допускає ні лінійних переміщень, ні поворотів затисненого кінця балки. Жорстке закладення замінюють реактивною силою, не відомою по модулю і напряму, і реактивним моментом (три невідомих). Реактивну силу, невідому по напряму, розкладають на дві взаємно перпендикулярні складові.
Якщо при рішенні задач реактивна сила або реактивний момент виходить негативною, то їх дійсний напрям протилежний прийнятому на малюнку.
Окрім перерахованих вище за три основні типи опор балок в конструкціях нерідко балка вільно спирається на площину (поверхня) або на ребро призми. В цьому випадку реакція опори направлена по нормалі до поверхні тіла у бік тіла, оскільки нормаль до поверхні тіла є єдиний напрям переміщення, яке не допускають ці зв'язки (одне невідоме).
Для визначення реакцій опор використовують умови рівноваги плоскої системи довільно розташованих сил:



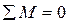
Список літератури
1.Эрдеди А.А., Медведев Ю. А., Эрдеди Н. А., Техническая механика, М., Высша школа, 1991, с.33 - 34
2.Мовнин М. С., Израелит А. Б.,Рубашкин А. Р., Руководство к решению задач по технической механике, М. Высшая школа, 1977, с.20-28
Практична робота №4
Визначення центру тяжіння плоских перетинів.
Мета роботи: виконати аналіз плоского перетину і визначити координати центру тяжіння.
Хід роботи
1. Перекреслити заданий перетин.
2. Виконати аналіз заданого перетину і розрахункову схему.
3. Намітити структуру рішення задачі.
4. Визначити координати центрів тяжіння і площі простих перетинів.
5. Визначити координати центру тяжіння складного перетину.
6. Оформити звіт, який містить:
- тему;
- мету роботи;
- умову завдання і розрахункову схему;
- аналіз заданого перетину;
- рішення задачі;
- висновок.
Контрольні питання
1. Чи можна розглядати силу тяжіння як рівнодіючу системи паралельних сил?
2. Чи може центр тяжіння розташовуватися поза самим тілом?
3. Як визначається центр тяжіння складної фігури, що складається з декількох простих?
4. Як слід раціонально проводити розбиття фігури складної форми на прості фігури при визначенні центру тяжіння всієї фігури?
5. Який знак має площа отвору у формулі для визначення центру тяжіння?
6. На перетині яких ліній трикутника знаходиться його центр тяжіння?
7. Якщо фігуру важко розбити на невелике число простих фігур, який спосіб визначення центру тяжіння може дати найбільш швидку відповідь?






