Конспект - 1
КІРІСПЕ
Механиканың құрылымы мен негізгі анықтамалары
механика – материя қозғалысының ең қарапайым түрі - механикалық қозғалыстың болу, өзгеру себептерін және қозғалыс заңдылықтарын зерттейтін ілім.
механикалық қозғалыс - уақыт өтуімен денелердің немесе бір дененің бөліктерінің кеңістікте бір-біріне қатысты орны өзгеруі.
классикалық механика (галилей -ньютон механикасы) – жылдамдығы вакуумдегі жарықтың таралу жылдамдығымен салыстырғанда анағұр-лым аз макроскопиялық денелердің қозғалыс заңдылықтарын зерттейді.
релятивистік механика – жылдамдықтары вакуумдегі жарықтың таралу жылдамдығымен шамалас макроскопиялық денелердің қозғалыс заңдылықтарын зерттейді (а.эйнштейн тұжырымдаған арнаулы салыстырмалылық теориясына негізделген).
кванттық механика – микроскопиялық денелердің (жеке атомдардың, элементар бөлшектердің, т.б.) қозғалыс заңдарын зерттейді.
механиканың бөлімдері:
кинематика – денелердің қозғалыс заңдарын қозғалыстың болу және өзгеру себептеріне байланыссыз зерттейді;
динамика – денелердің өзара әсерлесуінің олардың механикалық қозғалысына ықпалын, қозғалыс заңдарын қозғалыстың пайда болу және өзгеру себептерімен байланыстырып зерттейді;
статика – денелер жүйесінің тепе-теңдікте болу шарттарын зерттейді. егер дененің қозғалыс заңы белгілі болса, одан дененің тепе-теңдікте болу заңы мен шарттарын анықтауға болады.
механикада денелер қозғалысын суреттеу үшін нақты есеп шартына байланысты әртүрлі физикалық модельдер қолданылады:
материалдық нүкте – берілген есеп шартында өлшемдері ескерілмейтін массасы бар дене;
материалдық нүктелер жүйесі – әрқайсысы материалдық нүкте деп қарастырылатын өзара әсерлесуде болатын денелердің немесе кез келген макроскопиялық дененің бөліктерінің жиыны. механикада алдымен жеке материалдық нүктенің қозғалысы қарастырылып, зерттеу нәтижесі нүктелер жиынының қозғалысына қолданылады.
абсолют қатты дене – ешқандай жағдайда деформацияланбайтын, барлық уақытта шартты алынған екі нүктесінің ара қашықтығы тұрақты болатын дене. өзара қатаң байланыстағы материалдық нүктелер жүйесін абсолют қатты дене ретінде қарастыруға болады.
абсолют серпімсіз дене – сыртқы күштердің денеге әсері тоқтағанда (жойылғанда) деформацияланған күйі толығымен сақталатын дене;
абсолют серпімді дене – сыртқы күш әсері тоқтағанда бұрынғы пішіні мен өлшемдері толығымен қалпына келетін дене. осындай шартта денелердің деформациясы гук заңымен сипатталады.
Кинематика
кеңістікте қозғалыстағы немесе тыныштық күйдегі денелердің орнын анықтауда таңдап алынған салыстыру денесі санақ денесі деп аталады.
|

1-сурет
материалдық нүктенің орны координаттардың декарттық жүйесінде x, y, z координаттармен немесе  радиус-вектормен анықталады (1-сурет):
радиус-вектормен анықталады (1-сурет): 
қозғалыстағы материалдық нүктенің координаттары уақыт өтуімен өзгеріп отырады. жалпы жағдайда, нүктенің қозғалысы
x=x(t), y=y(t), z=z(t), (1)
скалярлық теңдеулер жүйесімен, немесе оған балама
 (2)
(2)
векторлық теңдеумен анықталады. (1) және (2) теңдеулер материалдық
нүкте қозғалысының кинематикалық теңдеуі деп аталады.
|
қозғалыстағы материалдық нүктенің (немесе дененің) берілген санақ жүйесінде сызған ізі – траектория. траекторияның пішініне қарай дененің қозғалысын түзу сызықты және қисық сызықты деп бөледі. дененің кез келген екі нүктесін қосатын түзу қозғалыс кезінде өзінің бастапқы жағдайына параллель орын ауыстырса, дененің қозғалысы ілгерілемелі деп аталады.

|
2-сурет
нүктенің берілген уақыт сәтіндегі қозғалыс шапшаңдығы мен бағыты жылдамдықпен сипатталады. материалдық нүктенің радиус–векторы өсімшесінің  осы өзгеріс болған
осы өзгеріс болған 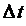 уақыт аралығына қатынасы орташа жылдамдық деп аталады:
уақыт аралығына қатынасы орташа жылдамдық деп аталады: 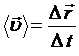 (3)
(3)
|
орташа жылдамдық векторы орын ауыстыру векторымен бағыттас болады (3-cурет). уақыттың берілген сәтіндегі немесе траекторияның

|
3-сурет
лездік жылдамдықтың модулі жолдың уақыт бойынша алынған бірінші туындысымен анықталады:
 (5)
(5)
айнымалы қозғалыстағы дене жылдамдығының модулі мен бағыты-ның қаншалықты тез өзгеретінін сипаттайтын шама – үдеу. жылдамдық өзгерісінің сол өзгеріс болған уақыт аралығына қатынасымен анықталатын векторлық шама орташа үдеу деп аталады:
 (6)
(6)
|

|
материалдық нүктенің берілген t уақыт мезетіндегі лездік үдеуі орташа үдеудің шегіне тең:  (7)
(7)
4-сурет
толық үдеуі тангенциал және үдеуі нормаль үдеулердің геометриялық қосындысына тең:


 (8)
(8)
материалдық нүктенің t1 -ден t2 -ге дейінгі уақыт аралығында жүрген жолын анықтау үшін  функциясын білу керек:
функциясын білу керек:
 (9)
(9)
бірқалыпты қозғалған нүктенің t уақытта жүрген жолы:

бірқалыпты үдемелі қозғалған нүктенің t уақытта жүрген жолы:

|

|
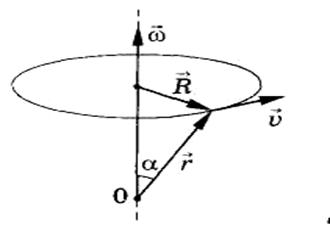
материалдықнүктенің қозғалмайтын оське қатысты радиусы r шеңбер бойымен айналмалы қозғалысында (5-сурет) бұрыштық орын
5-сурет

|
уақыт бойынша бірінші туындысына тең векторлық шама:
|
 . (10)
. (10)
6-сурет
нүктенің сызықтық және бұрыштық жылдамдықтары векторларының арасындағы байланыс:
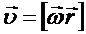 . (12)
. (12)
|
|
7-сурет 8-cурет
қозғалмайтын айналу осі маңайында айналып тұрған нүктенің орнын ось бойындағы кез келген о нүктесіне қатысты  радиус-вектормен анықтағанда (7-cурет), оның сызықтық жылдамдығының модулі:
радиус-вектормен анықтағанда (7-cурет), оның сызықтық жылдамдығының модулі:

бұрыштық үдеу бұрыштық жылдамдықтың уақыт бойынша бірінші туындысына тең векторлық шама:  (13)
(13)
үдемелі айналмалы қозғалыста бұрыштық үдеу векторы 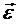 бұрыштық
бұрыштық
жылдамдық  векторымен бағыттас, кемімелі қозғалыста оған қарама-қарсы болады (8-сурет).
векторымен бағыттас, кемімелі қозғалыста оған қарама-қарсы болады (8-сурет).
сызықтық және бұрыштық шамалар арасындағы байланыс:
 ;
;  . (14)
. (14)
 ;
;  . (15)
. (15)
мұндағы:
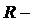 шеңбер радиусы;
шеңбер радиусы;  сызықтық жылдамдық;
сызықтық жылдамдық;  тангенциал үдеу;
тангенциал үдеу;  нормаль үдеу;
нормаль үдеу;  бұрыштық жылдамдық.
бұрыштық жылдамдық.
бақылау сұрақтары
1. материалдық нүкте деген не? санақ жүйесі деген не?
2. жол, траектория, орын ауыстыру деген не?
3. ілгерілемелі қозғалыс, айналмалы қозғалыс деген не?
4. лездік жылдамдық деген не? оның бағыты қалай анықталады?
5. үдеудің тангенциал және нормаль құраушылары нені анықтайды?
6. бұрыштық орын ауыстыру, бұрыштық жылдамдық, бұрыштық үдеу деген не? олардың бағыттары қалай анықталады?
7. сызықтық және бұрыштық шамалар арасындағы байланыс.
2-тақырып. материалдық нүкте мен қатты дененің





 уақыт арасында жүрген жолы
уақыт арасында жүрген жолы 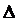 s деп аталады. Жол –уақыт-тың скаляр функциясы:
s деп аталады. Жол –уақыт-тың скаляр функциясы:
 Қозғалыстағы нүктенің бастапқы орнынан берілген уақыт сәтіндегі орнына жүргізілген
Қозғалыстағы нүктенің бастапқы орнынан берілген уақыт сәтіндегі орнына жүргізілген  вектор орын ауыстыру деп аталады (2-сурет). Түзу сызықты қозғалыста орын ауыстыру векторы траек-торияның сәйкес бөлігіне сай келеді, модулі нүктенің жүрген жолына тең:
вектор орын ауыстыру деп аталады (2-сурет). Түзу сызықты қозғалыста орын ауыстыру векторы траек-торияның сәйкес бөлігіне сай келеді, модулі нүктенің жүрген жолына тең:
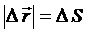 .
.
 (4)
(4)
 дене жылдамдығының модулінің өзгерісін (бағыты траекторияға жанама бойымен), ал нормаль құраушысы
дене жылдамдығының модулінің өзгерісін (бағыты траекторияға жанама бойымен), ал нормаль құраушысы  жылдамдықтың бағыты бойынша өзгерісін сипаттайды (бағыты траекторияның қисықтық центріне қарай).
Қисық сызықты қозғалыстағы нүктенің
жылдамдықтың бағыты бойынша өзгерісін сипаттайды (бағыты траекторияның қисықтық центріне қарай).
Қисық сызықты қозғалыстағы нүктенің
 бұрылулар (шексіз өте аз) векторы ретінде қарастырылады. Осы вектордың модулі радиустың бұрылу бұрышына тең, ал бағыты нүктенің айналуына сәйкес бұралатын бұранда ұшының ілгеріле-мелі қозғалыс бағытымен (оң бұранда ережесі бойынша)анықталады.
Айналыстың бұрыштық жылдамдығы
бұрыштық
бұрылулар (шексіз өте аз) векторы ретінде қарастырылады. Осы вектордың модулі радиустың бұрылу бұрышына тең, ал бағыты нүктенің айналуына сәйкес бұралатын бұранда ұшының ілгеріле-мелі қозғалыс бағытымен (оң бұранда ережесі бойынша)анықталады.
Айналыстың бұрыштық жылдамдығы
бұрыштық 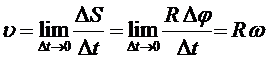 (11)
(11)


