Тема 1. Матрицы
1. Основные понятия. Л и т е р а т у р а. [1], §1, п.1.1.
2. Действия над матрицами. Л и т е р а т у р а. [1], §1, п.1.2.
Тема 2. Определители
1. Основные понятия. Л и т е р а т у р а. [1], §2, п.2.1.
2. Свойства определителей. Л и т е р а т у р а. [1], §2, п.2.2.
Тема 3. Системы линейных алгебраических уравнений
1. Основные понятия. Л и т е р а т у р а. [1], §4, п.4.1.
2. Решение систем линейных уравнений. Л и т е р а т у р а. [1], §4, п.4.2.
3. Матричный метод решения систем линейных уравнений. Формулы Крамера. Л и т е р а т у р а. [1], §4, п.4.3.
4. Решение систем линейных уравнений методом Гаусса.
Л и т е р а т у р а. [1], §4, п.4.4.
Тема 4. Векторы
1. Основные понятия. Л и т е р а т у р а. [1], §5, п.5.1.
2. Линейные операции над векторами. Л и т е р а т у р а. [1], §5, п.5.2.
3. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы. Действия над векторами, заданными проекциями. Л и т е р а т у- р а. [1], §5, п.5.3.-5.5.
Тема 5. Скалярное произведение векторов
1. Определение скалярного произведения. Л и т е р а т у р а. [1], §6 п.6.1.
2. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Л и т е р а т у р а. [1], §6, п.6.2.,6.3.
3. Приложение скалярного произведения. Л и т е р а т у р а. [1], §6, п.6.4.
Тема 6. Векторное произведение векторов
1. Определение векторного произведения. Л и т е р а т у р а. [1], §7, п.7.1.
2. Свойства векторного произведения. Выражение векторного произведения через координаты. Л и т е р а т у р а. [1], §7, п. 7.2., 7.3.
3. Приложение векторного произведения. Л и т е р а т у р а. [1], §7, п. 7.4.
Тема 7. Смешанное произведение векторов
1. Определение смешанного произведения. Л и т е р а т у р а. [1], §8, п.8.1.
2. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Л и т е р а т у р а. [1], §8, п.8.2., 8.3.
3. Приложение смешанного произведения. Л и т е р а т у р а. [1], §8, п. 8.4.
Тема 8. Линии на плоскости
1. Прямая линия на плоскости. Л и т е р а т у р а. [1], §10, п.10.2., 10.3.
2. Линии второго порядка на плоскости. Л и т е р а т у р а. [1], §11, п.11.1.-11.5.
Тема 9. Аналитическая геометрия в пространстве
1. Плоскость в пространстве. Л и т е р а т у р а. [1], §12, п.12.2, 12.3.
2. Прямая линия в пространстве. Л и т е р а т у р а. [1], §12; [2], п. 12.4. – 12.6.
3. Поверхности второго порядка. Л и т е р а т у р а. [1], §12, п.12.7.,12.8.
Тема 10. Введение в анализ
1. Функция: основные понятия. Л и т е р а т у р а. [1], §14, п.14.1-14.6.
2. Предел функции. Л и т е р а т у р а. [1], §16, п.16.1-16.3.
3. Основные теоремы о пределах. Первый и второй замечательные пределы. Л и т е р а т у р а. [1], §16, п.17.3, 17.5., 17.6.
4. Непрерывность функции. Л и т е р а т у р а. [1], §19, п.19.1-19.5.
Тема 11. Производная и дифференциал
1. Производная функции (определение, свойства, правила дифференцирования). Л и т е р а т у р а. [1], §20, п. 20.1-20.6.
2. Производные высших порядков. Л и т е р а т у р а. [1], §23, п.23.1, 23.2.
3. Дифференциал функции. Л и т е р а т у р а. [1], §24, п. 24.1-24.6.
Тема 12. Исследование функций с помощью производной
1. Правила Лопиталя. Л и т е р а т у р а. [1], §25, п.25.2.
2. Возрастание и убывание функции. Экстремумы. Л и т е р а т у ра. [1], §25, п. 25.3., 25.4.
3. Выпуклость графика функции. Точки перегиба. Л и т е р а т у ра. [1], §25, п. 25.6.
4. Асимптоты графика функции. Общая схема исследования функции и построение графиков. Л и т е р а т у р а. [1], §25, п. 25.7., 25.8.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Ниже приведена таблица номеров задач, входящих в контрольную работу №1, которая выполняется студентами в первом семестре. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его учебного номера (зачетной книжки, студенческого билета).
| Вариант | Номера задач |
| 1 11 21 31 41 2 12 22 32 42 3 13 23 33 43 4 14 24 34 44 5 15 25 35 45 6 16 26 36 46 7 17 27 37 47 8 18 28 38 48 9 19 29 39 49 10 20 30 40 50 |
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена вотдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в университет и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по каждому варианту. Контрольные работы, содержащие не все задачи или задачи не своего варианта, не засчитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие. Если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
ВОПРОСЫ К ЗАЧЕТУ
1. Определители второго и третьего порядков, их свойства и способы вычисления.
2. Матрицы. Операции над матрицами.
3. Решение систем линейных алгебраических уравнений по правилу Крамера и матричным способом.
4. Векторы. Основные понятия. Операции над векторами.
5. Прямоугольная система координат. Операции над векторами в координатной форме.
6. Скалярное произведение двух векторов, его свойства. Выражение его в координатной форме.
7. Векторное произведение двух векторов, его свойства. Выражение его в координатной форме.
8. Смешанное произведение трех векторов, его свойства. Выражение его в координатной форме.
9. Уравнения плоскости (общее, в отрезках) в пространстве.
10. Уравнения прямой в пространстве (каноническое, параметрическое, векторное).
11. Определение функции и способы ее задания.
12. Определение предела функции при стремлении аргумента к некоторому конечному пределу и предела функции при стремлении аргумента к бесконечности.
13. Определение непрерывности функции в точке и на отрезке. Точки разрыва функций.
14. Определение производной. Геометрический и механический смыслы.
15. Формулы производных суммы, произведения, частного двух функций.
16. Таблица производных элементарных функций.
17. Правило дифференцирования сложной функции.
18. Определение экстремума. Необходимое и достаточное условия.
19. Общая схема исследования функции и построение ее графика.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
1-10. Решить систему линейных уравнений: 1) по правилу Крамера; 2) с помощью обратной матрицы.
1. 
 2.
2. 
3.  4.
4. 
5.  6.
6. 
7. 
 8.
8. 
9. 
 10.
10. 
11-20. Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4.; 3) площадь грани А1А2А3; 4) объем пирамиды; 5) уравнения прямой А1А2; 6) уравнение плоскости А1А2А3; 7) угол между ребром А1А4 и гранью А1А2А3. Сделать чертеж.
11. А1 (-2; 1; 2), А2 (4; 2; 5), А3 (0; 2; 7), А4 (1; 3; 2).
12. А1 (4; 0; 0), А2 (-2; 1; 2), А3 (1; 3; 2), А4 (3; 2; 7).
13. А1 (-2; 1; 2), А2 (4; 0; 0), А3 (3; 2;7), А4 (1; 3; 2).
14. А1 (1; 3; 2), А2 (3; 2; 7), А3 (4; 0;0), А4 (-2; 1; 2).
15. А1 (3; 2; 7), А2 (1; 3; 2), А3 (-2; 1; 2), А4 (4; 0; 0).
16. А1 (3; 1; -2), А2 (1; -2; 1), А3 (-2; 1; 0), А4 (2; 2; 5).
17. А1 (1; -2; 1), А2 (3; 1; -2), А3 (2; 2; 5), А4 (-2; 1; 0).
18. А1 (-2; 1; 0), А2 (2; 2; 5), А3 (3; 1; 2), А4 (1; -2; 1).
19. А1 (2; 2; 5), А2 (-2; 1; 0), А3 (1; -2; 1), А4 (3; 1; 2).
20. А1 (1; -1; 6), А2 (4; 5; -2), А3(-1; 3; 0), А4 (6; 1; 5).
21-30. Найти пределы функций.
21. 

22. 

23. 

24. 

25. 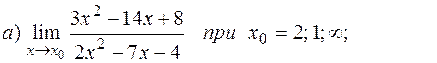

26. 

27. 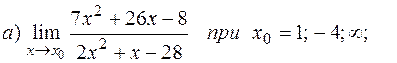

28. 

29. 

30. 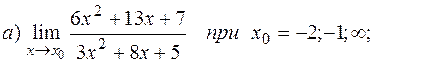

31-40. Найти производные заданных функций y=f(x).
31. а) y = (6x-1)2+  ; б)
; б)  ;
;
в) 
32. а) y = (3-2x)2+  ; б)
; б)  ;
;
в) 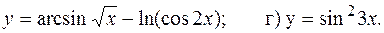
33. а) y = (2+5x)2+  ; б)
; б)  ;
;
в) 
34. а) y = (4x+1)3+  ; б)
; б)  ;
;
в) 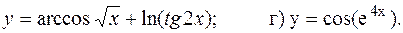
35. а) y = (3+7x)2+  ; б)
; б)  ;
;
в) 
36. а) y = (2-7x)3+ln( ); б)
); б)  ;
;
в) 
37. а) y = (1+6x)3+  ; б)
; б)  ;
;
в) 
38. а) y = (10x+5)7+  ; б)
; б)  ;
;
в) 
39. а) y = (7+2x)10+  ; б)
; б)  ;
;
в) 
40. а) y = (3x-2)8+  ; б)
; б)  ;
;
в) 
41-50. Исследовать методами дифференциального исчисления функцию y=f(x) и, используя результаты исследования, построить ее график.
41.. 42..
43.. 44..
45.. 46..
47.. 48..
49.. 50..






