Изменение координат вектора при изменении базиса

Пусть в -мерном линейном пространстве выбран базис , который мы будем для удобства называть "старый" и другой базис , который мы будем называть "новый". Возьмем призвольный вектор из . Его координатный столбец в старом базисе обозначим , а в новом -- . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

Замечание 18.1 Матрица перехода всегда невырождена, то есть .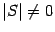

Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой

(18.1)

где справа стоит произведение матрицы перехода на матрицу-столбец.

Доказательство. Так как -- координатный столбец вектора в новом базисе, то

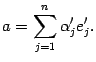
Заменив векторы их разложениями по старому базису, получим

В силу предложения 14.3 изменим порядок суммирования

Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца будет иметь такой же вид. Следовательно, формула (18.1) доказана.

Пример 18.4 Пусть , то есть -- трехмерное векторное пространство. Пусть задан ортонормированный базис i, j, k. Выберем другой (новый) базис

Возьмем вектор . Найдем его координаты в новом базисе.

Выпишем матрицу перехода, ее столбцы -- это координаты новых базисных векторов

Пусть -- координатный столбец вектора в новом базисе. Тогда

(18.2)

откуда

Найдем матрицу по формуле (14.14). Находим определитель

Находим алгебраические дополнения

Следовательно,

Находим координаты вектора

Таким образом, новые координаты вектора : , , , .

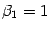Тот же самый результат можно было получить, записав формулу (18.2) в виде системы уравнений

Решив эту систему, например, методом Гаусса, найдем новые координаты , , .

 

 

Вперед: Матрица линейного преобразования Наверх: Линейные преобразования Назад: Линейные преобразования

Определение и примеры

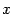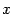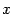Рассмотрим линейное пространство и преобразование этого пространства, то есть закон, по которому каждому вектору из соответствует вектор из того же пространства. Вектор называется образом вектора и обозначается , а вектор называется прообразом вектора .

Определение 19.1 Преобразование линейного пространства называется линейным, если для любых векторов 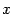и и любого числа выполнены равенства

(19.1)

то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.

Замечание 19.1 В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.

Линейное преобразование пространства называют также линейным отображением из в или линейным оператором из в .

Исходя из равенств (19.1) легко проверить, что

то есть образ линейной комбинации векторов равен линейной комбинации их образов.

Рассмотрим несколько примеров линейных преобразований.

Пример 19.1 Пусть -- двумерное векторное пространство, то есть множество векторов плоскости. Пусть . Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование можно представить как растяжение плоскости в два раза (рис. 19.1).

Рис.19.1.Преобразование растяжения

 

Проверим выполнение равенств (19.1)

Равенства (19.1) выполнены, следовательно, преобразование является линейным.

Пример 19.2 Пусть -- двумерное векторное пространство, -- поворот вектора по часовой стрелке на угол (рис. 19.2).

Рис.19.2.Преобразование поворота

 

Покажем, что это -- линейное преобразование.

Пусть 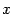и -- два вектора. Тогда -- это диагональ параллелограмма со стронами 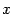, (рис. 19.3).

Рис.19.3.Образ суммы векторов

 

Если параллелограмм повернуть как единое целое на угол , то его стороны станут векторами и , диагональ будет вектором . С другой стороны, диагональ тоже повернулась на угол и поэтому является вектором 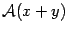. Следовательно, , первое из условий (19.1) выполнено.

Пусть -- число. Из рисунка 19.4 очевидно, что .

Рис.19.4.Образ вектора, умноженного на число

 

Следовательно, преобразование -- линейное.

 

Упражнение19.1.1. Пусть -- двумерное векторное пространство, -- некоторая прямая, проходящая через начало координат, -- преобразование, переводящее каждый вектор 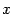в вектор симметричный исходному относительно прямой (рис. 19.5). Другими словами, является зеркальным отражением вектора 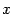в прямой .

Рис.19.5.Преобразование отражения

 

Докажите, что является линейным преобразованием.

 

Упражнение19.1.2. Пусть -- двумерное векторное пространство, -- некоторая прямая, проходящая через начало координат, -- преобразование, переводящее каждый вектор 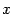в его проекцию на прямую (рис. 19.6).

Рис.19.6.Преобразование проектирования

 

Докажите, что является линейным преобразованием.

Пример 19.3 Пусть -- пространство всех многочленов, -- преобразование, которое переводит вектор из , то есть многочлен, в производную этого многочлена, которая естественно является многочленом, то есть вектором из . Пусть , то есть . Тогда

Например, если , то . Покажем, что преобразование является линейным.

Пусть , -- число. Тогда в силу свойства линейности производной получим

Аналогично,

Следовательно, -- линейное преобразование.

Пример 19.4 Пусть -- -мерное линейное пространство, Выберем в этом пространстве базис . Тогда у любого вектора 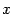есть его координатный столбец . Пусть -- квадратная матрица порядка . Определим преобразование следующим образом: является вектором, координатный столбец которого равен 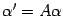(справа стоит произведение матрицы на столбец ). Покажем, что преобразование -- линейное.

Пусть 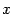и имеют координатные столбцы и соответственно, а их образы и -- координатные столбцы , и . Тогда

Но выражение в последнем равенстве справа является координатным столбцом образа суммы векторов . Следовательно, .

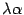Пусть -- произвольное число. Тогда координатный столбец вектора равен , координатный столбец образа вектора

то есть равен числу , умноженному на координатный столбец образа вектора 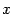. Поэтому . Тем самым мы доказали, что преобразование является линейным.

Очевидно, что примерами линейных преобразований могут служить тождественное преобразование, то есть преобразование, переводящее каждый вектор в себя, , и нулевое преобразование, переводящее каждый вектор в нуль, .

Легко проверяется, что для любого линейного преобразования образ нуля равен нулю, . Действительно, в силу второго из равенств (19.1)

Вперед: Матрица линейного преобразования Наверх: Линейные преобразования Назад: Линейные преобразования

Вперед: Координаты векторов Наверх: Линейные пространства Назад: Определение и примеры

Координаты векторов

Определение 18.4 Пусть -- -мерное линейное пространство, вещественное или комплексное, -- базис. Тогда произвольный вектор из представим в виде линейной комбинации векторов базиса:

Числа называются координатами вектора в базисе . Столбец из координат вектора называется координатным столбцом вектора .

Предложение 18.3 Координаты вектора в заданном базисе определяются однозначно.

Доказательство. Предположим противное. Пусть -- базис, в котором у вектора есть два различных набора координат:

Тогда

то есть

Так как наборы координат различны, то хотя бы один из коэффициентов справа отличен от нуля. Следовательно, векторы -- линейно зависимы, что противоречит определению базиса. Полученное противоречие означает, что предположение о наличии двух различных наборов координат неверно.

Предложение 18.4 Пусть в -мерном пространстве задан базис . Тогда координатный столбец суммы векторов равен сумме координатных столбцов слагаемых, координатный столбец произведения вектора на число равен координатному столбцу вектора, умноженному на это число.

Доказательство. Пусть векторы и имеют координатные столбцы и соответственно. Отсюда следует, что

Поэтому

Это равенство означает, что координатный столбец вектора имеет вид . Первая часть предложения доказана. Доказательство второй части предоставляем читателю.

Из последнего предложения следует, что как только в -мерном пространстве зафиксирован базис, каждый вектор можно заменить его координатным столбцом, и операциям сложения и умножения на число соответствуют такие же операции над их координатными столбцами. Таким образом, каждое -мерное пространство является, с точки зрения алгебры, копией пространства в вещественном случае, а в комплексном -- копией .

 

Вперед: Изменение координат вектора при изменении базиса Наверх: Линейные пространства Назад: Базис и размерность пространства

Вперед: Евклидово пространство Наверх: Линейные пространства Назад: Координаты векторов