Определение 15.3. Дуга называется выпуклой, если она пересекается с любой своей секущей, не более чем в двух точках.
Если дуга выпуклая, то она лежит по одну сторону касательной в любой ее точке.
Будем рассматривать дуги, которые являются частями графика линий непрерывных функций. Линии, обращенные выпуклостью вверх, называются выпуклыми, а вниз – вогнутыми.
Определение 15.4. Точка на линии называется точкой перегиба, если она разделяет выпуклую дугу от вогнутой.
Пример 15.4. Рассмотрим 
: 
- точки перегиба.
Касательная в точке перегиба пересекает линию и параллельна Оу. Связь между второй производной 
и выпуклостью (вогнутостью) устанавливается следующими теоремами.
Теорема 15.4. (необходимый признак): Если дуга линии 
выпуклая, то 
(неположительная). Если дуга линии вогнутая, то 
(неотрицательная) в соответствующем интервале.
Теорема 15.5. (достаточный признак): Если всюду на некотором интервале, то дуга линии выпуклая. Если , то дуга – вогнутая.
Если 
- абсцисса точки перегиба, то 
, и меняет знак при переходе 
через . При перемене знака с «-» на «+» слева лежит выпуклый участок, а справа – вогнутый, с «+» на «-» - наоборот.
Асимптоты линий
Определение 15.5. Прямая линия 
называется асимптотой, , если расстояние от точки линии до прямой стремится к нулю при 
. Будем различать вертикальные и наклонные асимптоты.
1)Вертикальные асимптоты графика функции находятся так,
если 
то 
- вертикальные асимптоты. (Функция, стремящаяся к 
исследуется в окрестности точки , т.е. 
или 
).
2)Наклонные асимптоты.
Асимптота – это прямая, следовательно, ее уравнение 
, где 
, (15.1)
, (15.2)
Заметим, что если равенство (15.1) может осуществляться, а равенство (15.2) нет 
, тогда линия - асимптот не имеет.
Пример 15.6. Дана функция 
. Найти асимптоты.
Вертикальная асимптота: 
Наклонные асимптоты: : 
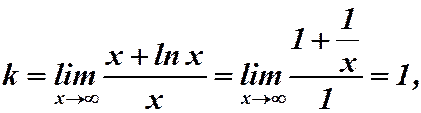
Наклонных асимптот нет.
Пример 15.7. Дана функция 
. Найти асимптоты.
Вертикальные: 
- вертикальные асимптоты. Наклонные: 
Следовательно, наклонные асимптоты 
(биссектриса I и III координатных углов).
Общая схема исследования функции
1) Область определения функции.
2) Точки разрыва и интервалы непрерывности.
3) Асимптоты.
4) Точки пересечения графика с осями координат.
5) Четность нечетность графика (симметрия графика).
6) Интервалы монотонности. Экстремумы и значения функции в экстремумах.
7) Интервалы выпуклости, вогнутости функции, точки перегиба.
Пример 15.8. Исследовать функцию и построить её график 
1. 
2. 
, точка разрыва II рода, т.к.
- интервалы непрерывности.
3. Наклонная 
; 
.
| х | ||
| у | -1 |
4. Точки пересечения графика с осями:
1) 
2) Если 
одна точка пересечения с осями координат.
Четность, нечетность.
- не является ни четной, ни нечетной, следовательно, график несимметричен ни относительно осей Ох и Оу, ни относительно начала координат .
6. Найдем производную: 
и приравняем ее к нулю: 
. критические точки; производ-ная 
.
Определим знак производной на каждом интервале:
Точка 
- максимум; 
Точка 
- минимум; 
.
7.Интервалы выпуклости, вогнутости функции, точки перегиба.
Найдем вторую производную:
Точек перегиба нет.
Так как 
, то на промежутке 
функция вогнута. Поскольку 
, то на промежутке 
функция выпуклая.
