Одно из самых важных назначений дифференциального исчисления – это применение его к исследованию функций (линий). Эта процедура опирается на весьма простую связь между поведением функции и свойствами ее производных.
Теорема 15.1.(Необходимый и достаточный признак монотонности).
1. Если функция 
в интервале возрастает, то её производная 
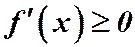- неотрицательная.
2. Если - убывает, то её производная неположительная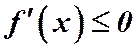 
.
3. Если 
, (то есть не изменяется), то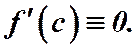 
Геометрический смысл теоремы
Если подвижная точка 
при движении по графику функции слева на право поднимается, то касательная к графику функции образует острый угол с осью Ох 
; если же точка опускается, то касательная образует тупой угол, 
.
В интервале монотонности функции знак её производной не может изменяться на противоположный.
Достаточный признак монотонности читается из теоремы в обратном порядке.
Пример 15.1. Исследовать на монотонность функцию: 
Решение: Найдем: 
Приравняем 
, то есть
.
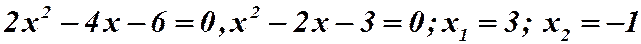Вся числовая ось разбивается на три интервала: 
1. 
функция возрастает;
2. 
функция убывает;
3. 
функция возрастает.
Определение 15.1. Те, значения 
, в которых производная обращается в нуль, называются стационарными точками функции.
Как видно из нашего примера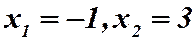 
- в этих точках функция меняет характер своего поведения, сначала возрастает, потом убывает и т.д.
Экстремумы функции
Определение 15.2. Точка 
называется точкой максимума функции , если 
, есть наибольшее значение функции в окрестности точки . Точка - минимум, если - наименьшее значение функции в окрестности точки . Точки максимум и минимум объединяются названием точки экстремума.
Необходимый признак экстремума функции
Теорема 15.2.(признак Ферма). Функция может иметь экстремумы только в тех точках, в которых ее производная равна нулю или не существует.
С геометрической точки зрения тот факт, что 
, по теореме Ролля означает, что касательная в точке х параллельна оси Ох, а тот факт, что 
- не существует, означает, что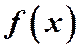 
- не дифференцируема (см. рисунки). Примеры таких функций:
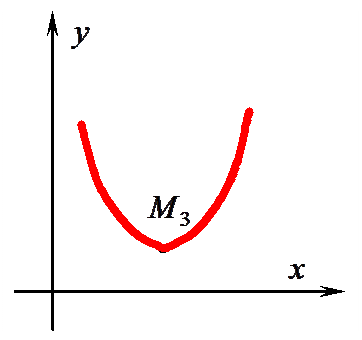
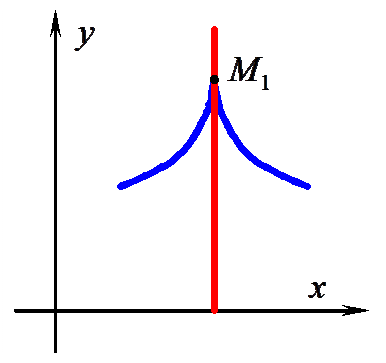
В точках 
и 
касательная параллельна оси Оу. Такие точки называются точками возврата.
В точках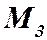 
и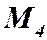 
касательная переходит внезапно от одного положения к другому, то есть, в этой точке нет, определенной касательной – угловые точки. Необходимый признак не является достаточным.
Пример 15.2.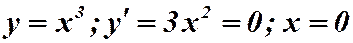 
, но производная не меняет знака, 
на всей числовой оси, следовательно, точка - не экстремум. Когда же точка будет экстремумом? Ответ на этот вопрос даёт следующая теорема.
