Примеры построения эпюр внутренних силовых факторов для консольных балок

При построении эпюр и 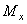в консольных, или жестко защемленных, балках нет необходимости вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 1.

Рассмотрим балку длиной l защемленную одним концом и находящуюся под действием сосредоточенной силы Р (рис.6.17). Пусть для определенности Р= 4 кН, l = 2 м.

Рис.6.17

 

Определим внутренние силовые факторы, возникающие в балке. Воспользуемся методом сечением.

Рассечем балку поперечным сечением в произвольном месте.

Отбросим правую часть.

Заменим ее действие внутренними усилиями N - вдоль оси z, - вдоль оси y и моментом 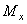– в плоскости осей yz вокруг оси х. На рис.6.17 в соответствии с принятым правилом знаков показаны положительные направления внутренних силовых факторов.

Уравновесим отсеченную часть. Запишем уравнения статического равновесия, получим

, ,

, , ,

, , .

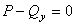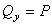Из первого уравнения видно, что нормальная сила N при изгибе равна нулю, далее не будем ее определять.

Построим эпюры поперечной силы Q_y и изгибающего момента M_x вдоль длины балки.

Поперечная сила постоянна по всей длине балки и равна Q_y = P = 4 кН. Отложим на графике линию параллельную оси z.

Изгибающий момент М_х изменяется в зависимости от расстояния z. Вычислим его значение в двух точках: в начале z = 0 и в конце балки z = l = 2 м.

z = 0 (М_х = 0);

z = 2 м (М_х = 8 кНм).

Построим по точкам график М_х.

Построение эпюр поперечной силы Q_y и изгибающего момента M_x является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Q_y и M_x определяется опасное сечение, т.е. сечение в котором может произойти разрушение.

Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения. .

В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила . В данном случае опасным является место закрепления балки.

Пример 2.

Построить эпюры и 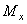(рис.6.18).

Рис. 6.18

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечную силу в каждом характерном сечении.

По вычисленным значениям строим эпюру .

3. Определяем изгибающий момент 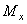в каждом характерном сечении.

По вычисленным значениям строим эпюру 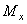, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

Пример 3.

Построить эпюры , 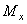(рис.6.19).

В данном случае для правильного построения эпюры 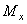необходимо использовать приведенные выше дифференциальные зависимости.

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечные силы в характерных сечениях.

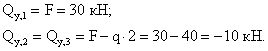
3. Строим эпюру .

Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент 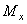будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.

Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки :

Рис. 6.19

 

Определяем изгибающие моменты в характерных сечениях.

4. Вычисляем экстремальное значение изгибающего момента в сечении, где :

Строим эпюру .